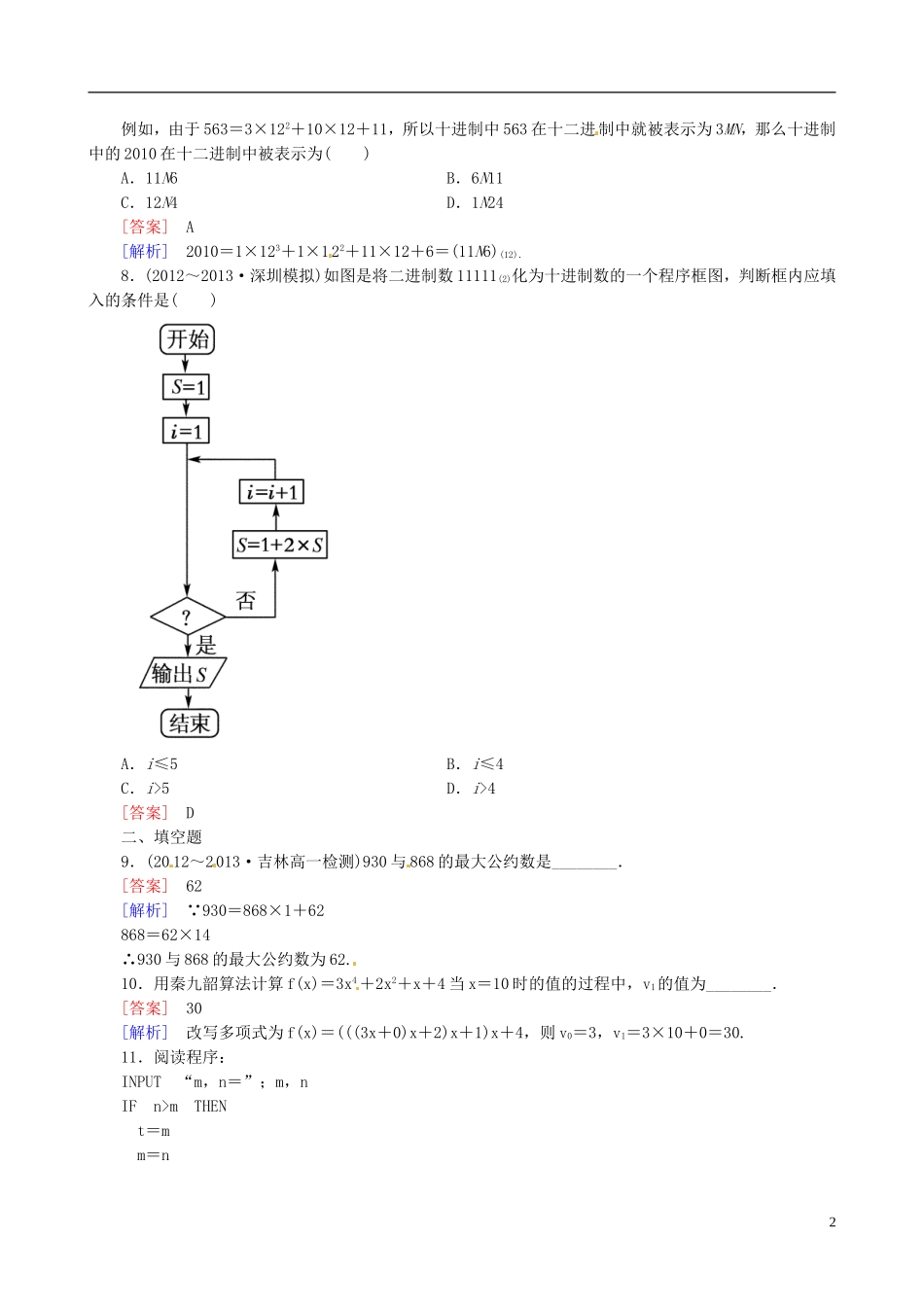
1. 3 算法案例 (练)一、选择题1.给出下列说法:①在计算机中,做一次乘法运算所用的时间,比做一次加法运算所用的时间长得多;②在计算机中,计算 xk(k=2,3,…,n)要进行 k 次运算;③因为秦九韶算法是在南宋时期提出的,所以现在在多项式求值中不是一种先进的算法;④利用秦九韶算法求 n 次多项式的值时,可以将其转化为求 n 个一次多项式的值,其中正确的个数是( )A.1 B.2C.3 D.4[答案] B[解析] ①④正确,②③不正确,故选 B.2.用更相减损术可求得 78 与 36 的最大公约数是( )A.24 B.18C.12 D.6[答案] D[解析] 先用 2 约简得 39,18;然后辗转相减得 39-18=21,21-18=3,18-3=15,15-3=12,12-3=9,9-3=6,6-3=3.所以所求的最大公约数为 3×2=6.3.用辗转相除法求 294 和 84 的最大公约数时,需要做除法的次数是( )A.1 B.2 C.3 D.4[答案] B[解析] 294=84×3+42,84=42×2,∴选 B.4.利用秦九韶算法计算多项式 f(x)=101x100+100x99+99x98+…+2x+1 当 x=x0时的值,其中下面公式 v0=101,vk=vk-1x0+101-k(k=1,2,…100)被反复执行,可用循环结构来实现,那么该循环结构中循环体被执行的次数为( )A.200 B.101 C.100 D.99[答案] C5.用秦九韶算法求多项式 f(x)=2x7+x6-3x5+4x3-8x2-5x+6 的值时,v5=v4x+( )A.-3 B.4 C.-8 D.-5[答案] C6.运行下面的程序,当输入 n=840 和 m=1764 时,输出结果是( )A.84 B.12 C.168 D.252[答案] A[解析] 1764=840×2+84,840=84×10,∴1764 与 840 的最大公约数为 84.7.类似于十进制中逢 10 进 1,十二进制的进位原则是逢 12 进 1,采用数字 0,1,2,…,9 和字母 M,N 共12 个计数符号,这些符号与十进制的对应关系如下表:十二进制0123456789MN十进制012345678910111例如,由于 563=3×122+10×12+11,所以十进制中 563 在十二进制中就被表示为 3MN,那么十进制中的 2010 在十二进制中被表示为( )A.11N6 B.6N11 C.12N4 D.1N24[答案] A[解析] 2010=1×123+1×122+11×12+6=(11N6)(12).8.(2012~2013·深圳模拟)如图是将二进制数 11111(2)化为十进制数的一个程序框图,判断框内应填入的条件是( )A.i≤5 B.i≤4C.i>5 D.i>4[答案] D二、填空题9.(20 12~2013·吉林高一检测)930 与 868 的最大公约数是_______...