3-1.3.1 秦九韶算法与排序(第三、四课时)

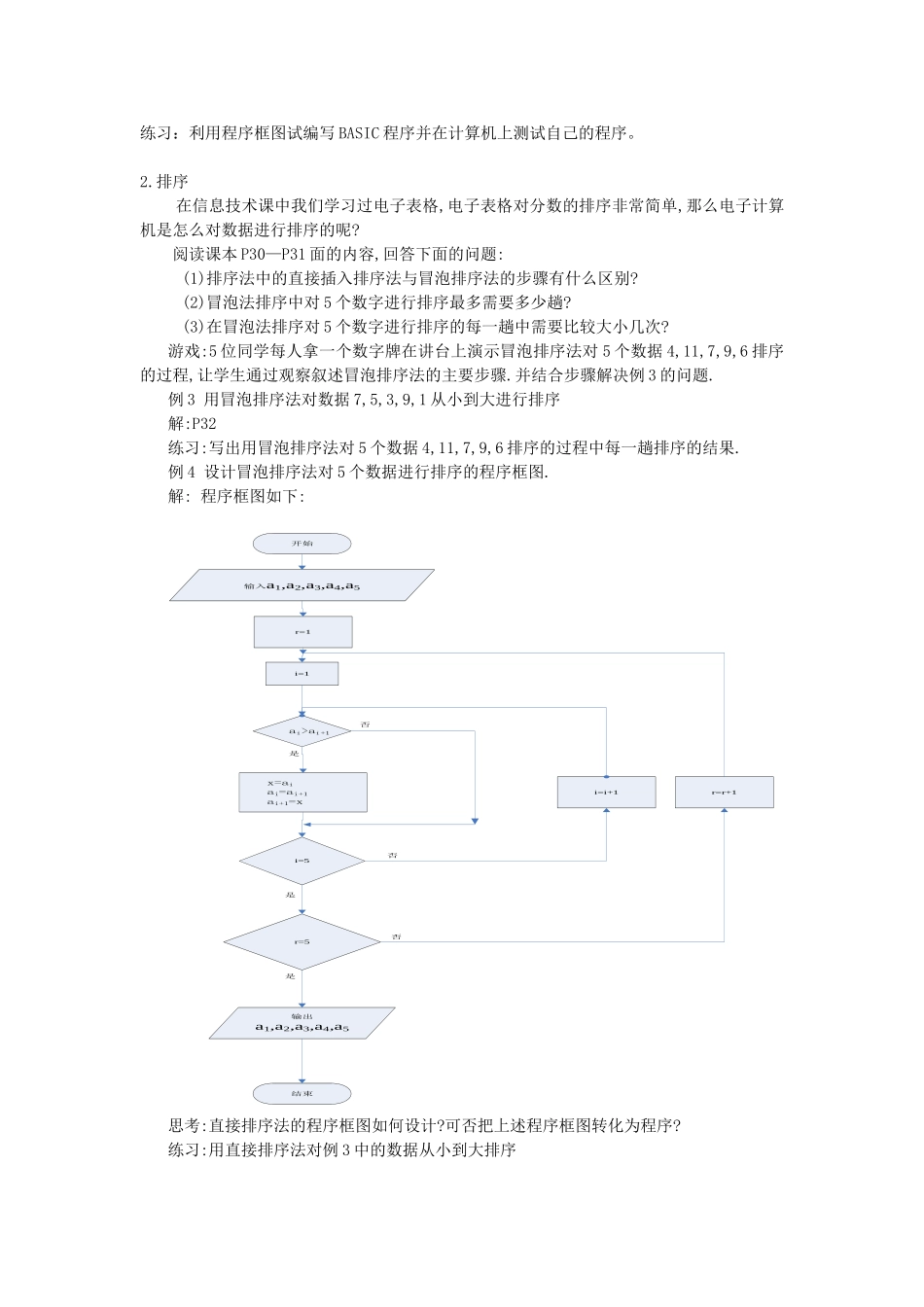
第三、四课时 秦九韶算法与排序一、三维目标（a）知识与技能1.了解秦九韶算法的计算过程，并理解利用秦九韶算法可以减少计算次数提高计算效率的实质。2.掌握数据排序的原理能使用直接排序法与冒泡排序法给一组数据排序，进而能设计冒泡排序法的程序框图及程序，理解数学算法与计算机算法的区别，理解计算机对数学的辅助作用。（b）过程与方法模仿秦九韶计算方法，体会古人计算构思的巧妙。能根据排序法中的直接插入排序法与冒泡排序法的步骤，了解数学计算转换为计算机计算的途径，从而探究计算机算法与数学算法的区别，体会计算机对数学学习的辅助作用。（c）情态与价值观通过对秦九韶算法的学习，了解中国古代数学家对数学的贡献，充分认识到我国文化历史的悠久。通过对排序法的学习，领会数学计算与计算机计算的区别，充分认识信息技术对数学的促进。二、教学重难点重点：1.秦九韶算法的特点2.两种排序法的排序步骤及计算机程序设计难点：1.秦九韶算法的先进性理解2.排序法的计算机程序设计三、学法与教学用具学法：1.探究秦九韶算法对比一般计算方法中计算次数的改变，体会科学的计算。2.模仿排序法中数字排序的步骤，理解计算机计算的一般步骤，领会数学计算在计算机上实施的要求。教学用具：电脑，计算器，图形计算器四、教学设计（一）创设情景，揭示课题我们已经学过了多项式的计算，下面我们计算一下多项式1)(2345xxxxxxf当5x时的值，并统计所做的计算的种类及计算次数。根据我们的计算统计可以得出我们共需要 10 次乘法运算，5 次加法运算。我们把多项式变形为：1)))1(1(1()(2xxxxxxf再统计一下计算当5x时的值时需要的计算次数，可以得出仅需 4 次乘法和 5 次加法运算即可得出结果。显然少了6 次乘法运算。这种算法就叫秦九韶算法。（二）研探新知1.秦九韶计算多项式的方法01210123120132211012211)))((())(()()(aaxaxaxaaxaxaxaxaaxaxaxaxaaxaxaxaxaxfnnnnnnnnnnnnnnnnnnn例 1 已知一个 5 次多项式为8.07.16.25.325)(2345xxxxxxf用秦九韶算法求这个多项式当5x时的值。解：略思考：（1）例 1 计算时需要多少次乘法计算？多少次加法计算？ （2）在利用秦九韶算法计算 n 次多项式当0xx 时需要多少次乘法计算和多少次加法计算？练习：利用秦九韶算法计算15.033.016.041.083....