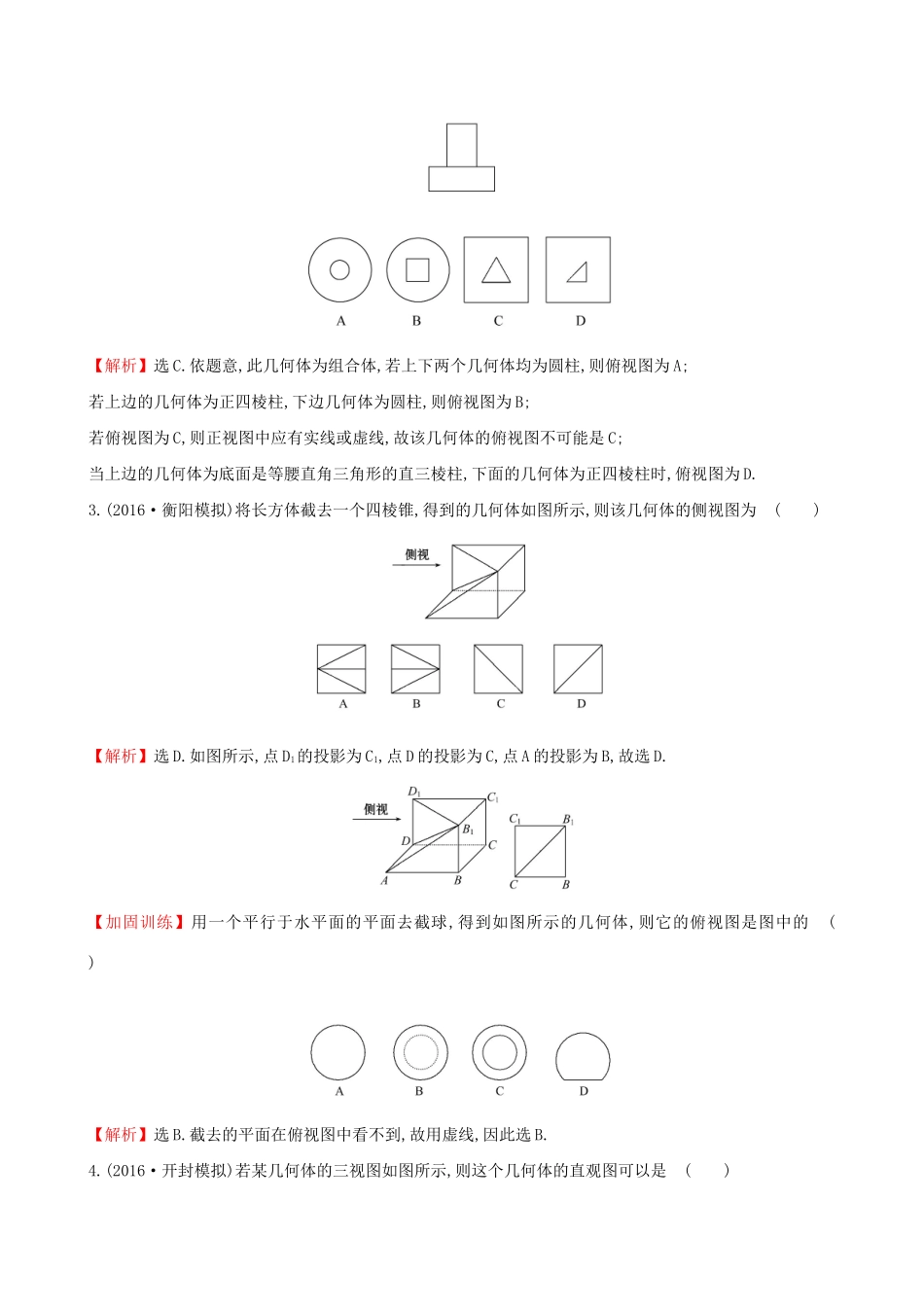
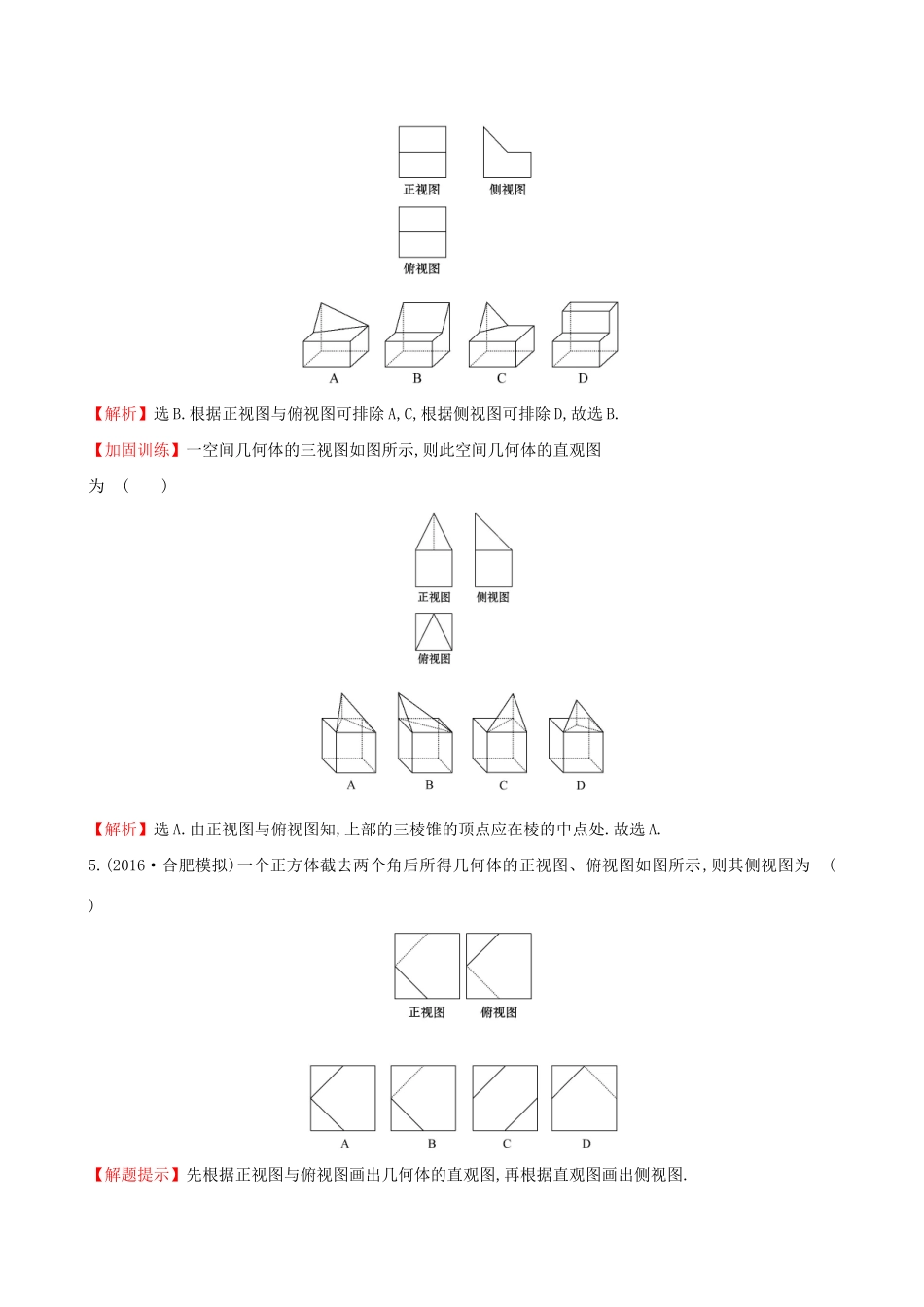
空间几何体的结构及其三视图和直观图(25分钟60分)一、选择题(每小题5分,共25分)1.下列结论正确的是()A.各个面都是三角形的几何体是三棱锥B.以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥C.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥D.圆锥的顶点与底面圆周上的任意一点的连线都是母线【解析】选D.A错误,如图所示,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是三棱锥;B错误,如图,若△ABC不是直角三角形或是直角三角形,但旋转轴不是直角边,所得的几何体都不是圆锥;C错误,若六棱锥的所有棱长都相等,则底面多边形是正六边形.由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长.2.已知某几何体的正视图和侧视图均如图所示,给出下列5个图形:其中可以作为该几何体的俯视图的图形个数是()A.5个B.4个C.3个D.2个【解析】选B.根据正视图与侧视图的画法知④不能作为俯视图,故选B.【加固训练】(2016·忻州模拟)某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是()【解析】选C.依题意,此几何体为组合体,若上下两个几何体均为圆柱,则俯视图为A;若上边的几何体为正四棱柱,下边几何体为圆柱,则俯视图为B;若俯视图为C,则正视图中应有实线或虚线,故该几何体的俯视图不可能是C;当上边的几何体为底面是等腰直角三角形的直三棱柱,下面的几何体为正四棱柱时,俯视图为D.3.(2016·衡阳模拟)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为()【解析】选D.如图所示,点D1的投影为C1,点D的投影为C,点A的投影为B,故选D.【加固训练】用一个平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是图中的()【解析】选B.截去的平面在俯视图中看不到,故用虚线,因此选B.4.(2016·开封模拟)若某几何体的三视图如图所示,则这个几何体的直观图可以是()【解析】选B.根据正视图与俯视图可排除A,C,根据侧视图可排除D,故选B.【加固训练】一空间几何体的三视图如图所示,则此空间几何体的直观图为()【解析】选A.由正视图与俯视图知,上部的三棱锥的顶点应在棱的中点处.故选A.5.(2016·合肥模拟)一个正方体截去两个角后所得几何体的正视图、俯视图如图所示,则其侧视图为()【解题提示】先根据正视图与俯视图画出几何体的直观图,再根据直观图画出侧视图.【解析】选C.根据一个正方体截去两个角后所得几何体的正视图、俯视图可得几何体的直观图为:所以侧视图为:.二、填空题(每小题5分,共15分)6.如图所示,四边形A′B′C′D′是一水平放置的平面图形的斜二测画法的直观图,在斜二测直观图中,四边形A′B′C′D′是一直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y′轴平行,若A′B′=6,D′C′=4,A′D′=2,则这个平面图形的实际面积为.【解析】根据斜二测画法规则可知:该平面图形是直角梯形ABCD,且AB=6,CD=4.由于C′B′=A′D′=2.所以CB=4.故平面图形的实际面积为×(6+4)×4=20.答案:207.(2016·长沙模拟)已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为的矩形,则该正方体的正视图的面积等于.【解析】由题知此正方体的正视图与侧视图是一样的,正视图的面积与侧视图的面积相等,为.答案:8.一个建筑物上部为四棱锥,下部为长方体,且四棱锥的底面与长方体的上底面尺寸一样,已知长方体的长、宽、高分别为20m,5m,10m,四棱锥的高为8m,若按1∶500的比例画出它的直观图,那么直观图中,长方体的长、宽、高和四棱锥的高应分别为.【解题提示】由20m=2000cm,=4cm,同理可得宽、高、四棱锥的高.【解析】由20m=2000cm,=4cm,同理可得宽、高分别为1cm,2cm,四棱锥的高为1.6cm.答案:4cm,1cm,2cm,1.6cm三、解答题(每小题10分,共20分)9.已知:图①是截去一个角的长方体,试按图示的方向画出其三视图;图②是某几何体的三视图,试说明该几何体的构成.【解析】图①几何体的三视图为:图②所示的几何体是上面为正六棱柱、下面为倒立的正六棱锥的组合体.10.已知正三棱锥V-ABC的正视图和俯视图如图所示.(1)画出该三棱锥的侧视图和直观图.(2)求出侧视图的面积.【解析】(1)如图.(2)侧视图中VA===2.则S△VBC=×2×2=6.(20...