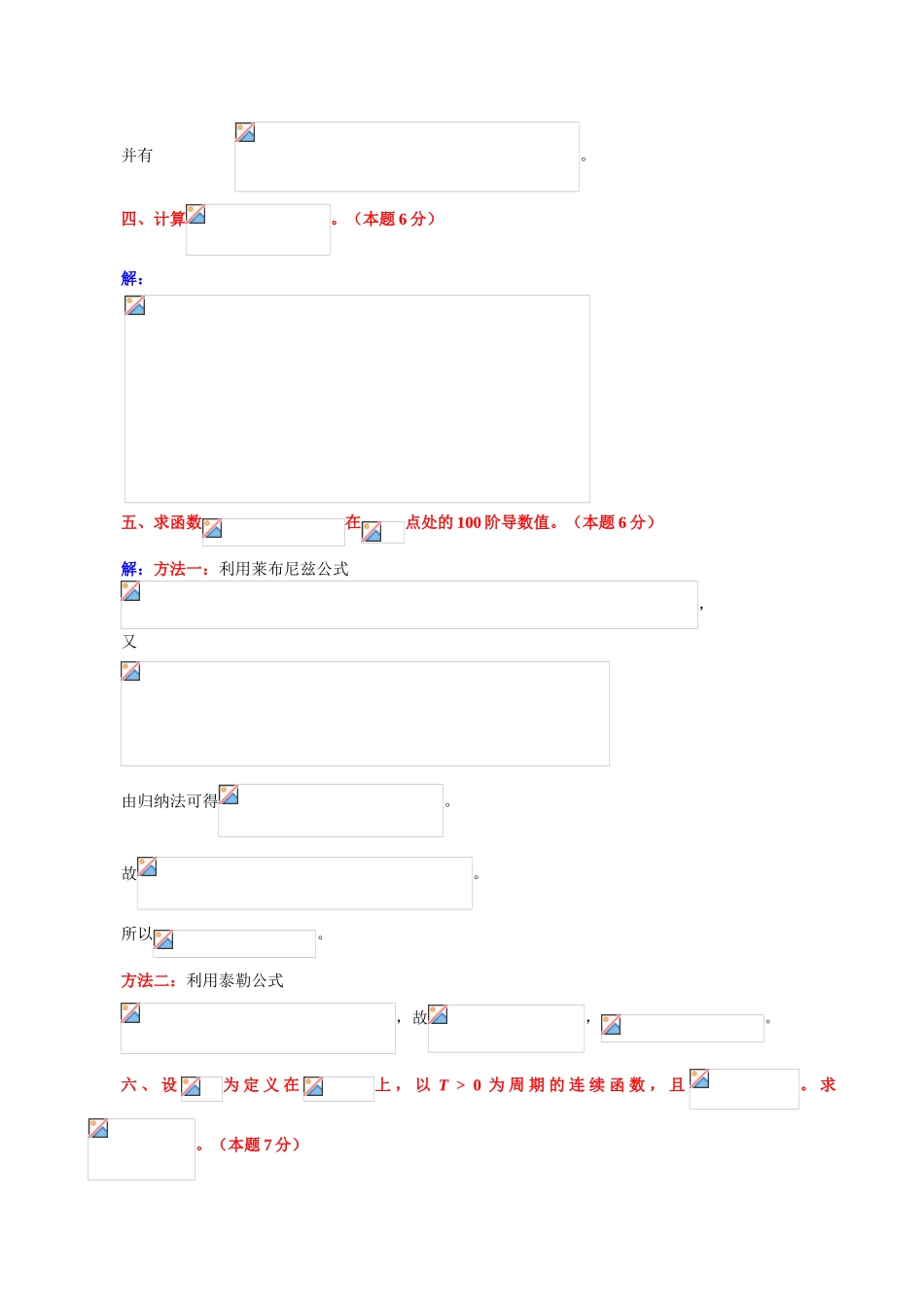
2024 年天津市大学数学竞赛试题参考答案(理工类)一、填空:(本题 15 分,每空 3 分。请将最终结果填在相应的横线上面。)1.设函数,则函数的定义域为 。2.设要使函数在区间上连续,则 。3.设函数由参数方程所确定,其中 f 可导,且,则 3 。4 . 由 方 程所 确 定 的 函 数在 点处 的 全 微 分 dz = 。5 . 设, 其 中 f 、具 有 二 阶 连 续 导 数 , 则 。二、选择题:(本题 15 分,每小题 3 分。每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。选对得分;选错、不选或选出的答案多于一个,不得分。)1. 已知,则( A )(A) 12; (B)3; (C) 1; (D)0。2. 设 函 数在的 一 个 邻 域 内 有 定 义 , 则 在点 处 存 在 连 续 函 数使是在点处可导的( C )(A)充分而非必要条件; (B)必要而非充分条件;(C)充分必要条件; (D)既非充分,也非必要条件。3. 设,则 F(x)=( D )(A) ; (B) ;(C) ; (D) 。4. 函数,在点处( B )(A)可微; (B)偏导数存在,但不可微;(C)连续,但偏导数不存在; (D)不连续且偏导数不存在。5. 设为区间上的正值连续函数,与为任意常数,区域,则( D )(A); (B); (C); (D)。三、设函数在点的某邻域内具有二阶导数,且。求:,,及。(本题 6 分)解:因为 ,所以 。由无穷小比较,可知 ,以及 。从而 ,其中,即 。由此可得 ,,。并有 。四、计算。(本题 6 分)解: 五、求函数在点处的 100 阶导数值。(本题 6 分)解:方法一:利用莱布尼兹公式,又由归纳法可得。故。所以。方法二:利用泰勒公式,故,。六 、 设为 定 义 在上 , 以 T > 0 为 周 期 的 连 续 函 数 , 且。 求。(本题 7 分)解:对于充分大的 x > 0,必存在正整数 n,使得。又 ,故有 ,及 。注意到: ,且当时,。由夹逼定理可知。七 、 在 椭 球 面上 求 一 点 , 使 函 数在 该 点 沿 方 向的方向导数最大。(本题 8 分)解: 函数的方向导数的表达式为。其中:为方向的方向余弦。因此。于是,根据题意,即求函数在条件下的最大值。设,则由得以及,即得驻点为与。因最大值必存在,故只需比较,,的大小。由此可知为所求。八、设正整数,证明方程至少有两个实根。(本题 6 分)...