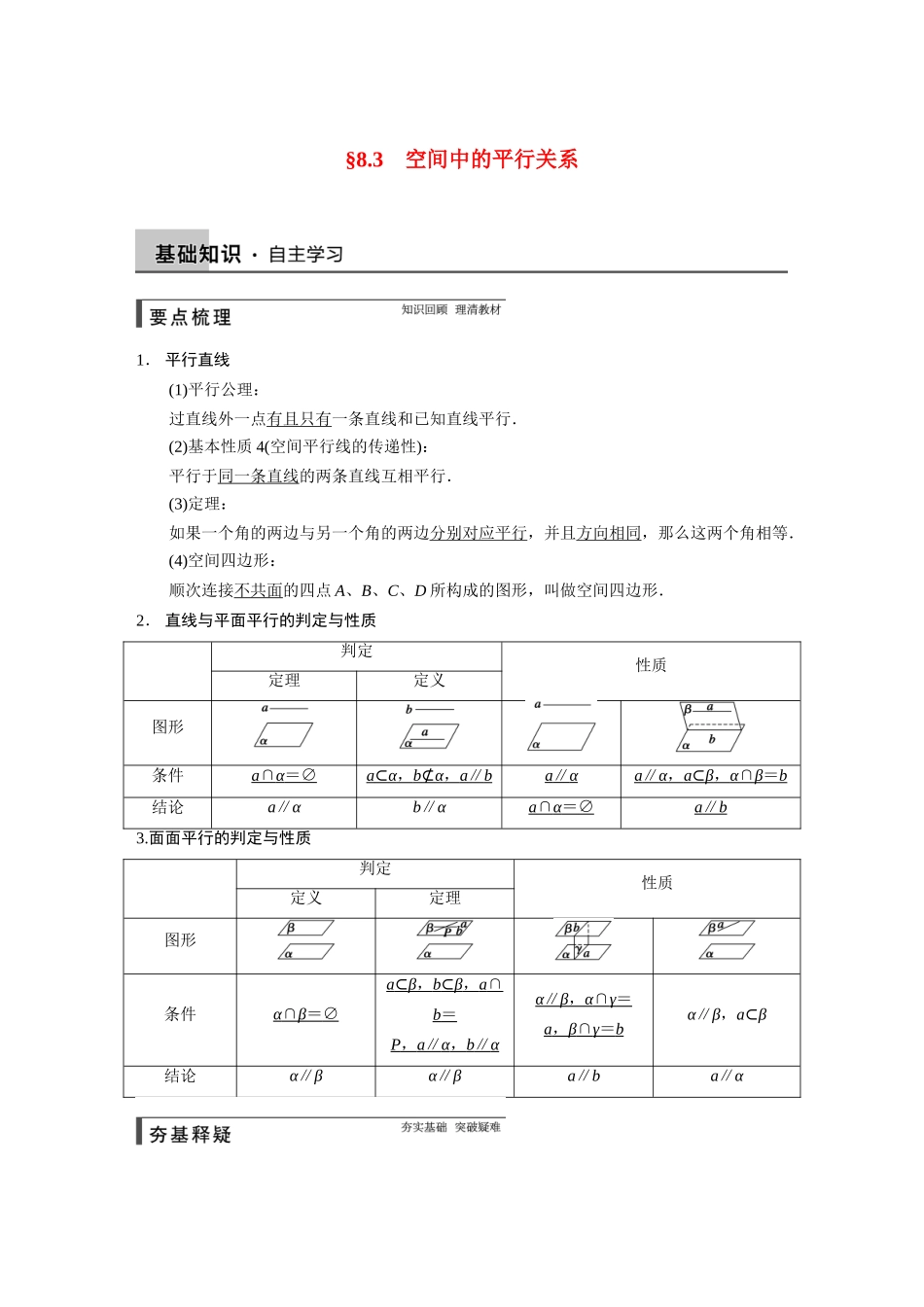
§8.3 空间中的平行关系1. 平行直线(1)平行公理:过直线外一点有且只有一条直线和已知直线平行.(2)基本性质 4(空间平行线的传递性):平行于同一条直线的两条直线互相平行.(3)定理:如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等.(4)空间四边形:顺次连接不共面的四点 A、B、C、D 所构成的图形,叫做空间四边形.2. 直线与平面平行的判定与性质判定性质定理定义图形条件a ∩ α = ∅ a ⊂ α , b ⊄ α , a ∥ b a ∥ α a ∥ α , a ⊂ β , α ∩ β = b 结论a∥αb∥αa ∩ α = ∅ a ∥ b 3.面面平行的判定与性质判定性质定义定理图形条件α ∩ β = ∅ a ⊂ β , b ⊂ β , a ∩ b = P , a ∥ α , b ∥ α α ∥ β , α ∩ γ = a , β ∩ γ = b α∥β,a⊂β结论α∥βα∥βa∥ba∥α1. 判断下面结论是否正确(请在括号中打“√”或“×”)(1)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.( × )(2)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( √ )(3)若直线 a 与平面 α 内无数条直线平行,则 a∥α.( × )(4)空间四边形 ABCD 中,E、F 分别是 AB,AD 的中点,则 EF∥平面 BCD.( √ )(5)若 α∥β,直线 a∥α,则 a∥β. ( × )2. 若直线 l 不平行于平面 α,且 l⊄α,则 ( )A.α 内的所有直线与 l 异面B.α 内不存在与 l 平行的直线C.α 内存在唯一的直线与 l 平行D.α 内的直线与 l 都相交答案 B解析 由题意知,直线 l 与平面 α 相交,则直线 l 与平面 α 内的直线只有相交和异面两种位置关系,因而只有选项 B 是正确的.3. 下列命题中,错误的是 ( )A.平面内一个三角形各边所在的直线都与另一个平面平行,则这两个平面平行B.平行于同一个平面的两个平面平行C.若两个平面平行,则位于这两个平面内的直线也互相平行D.若两个平面平行,则其中一个平面内的直线平行于另一个平面答案 C解析 由面面平行的判定定理和性质知 A、B、D 正确.对于 C,位于两个平行平面内的直线也可能异面.4. 如图,正方体 ABCD-A1B1C1D1中,AB=2,点 E 为 AD 的中点,点 F 在 CD 上.若 EF∥平面 AB1C,则线段 EF 的长度等于_____.答案 解析 因为直线 EF∥...