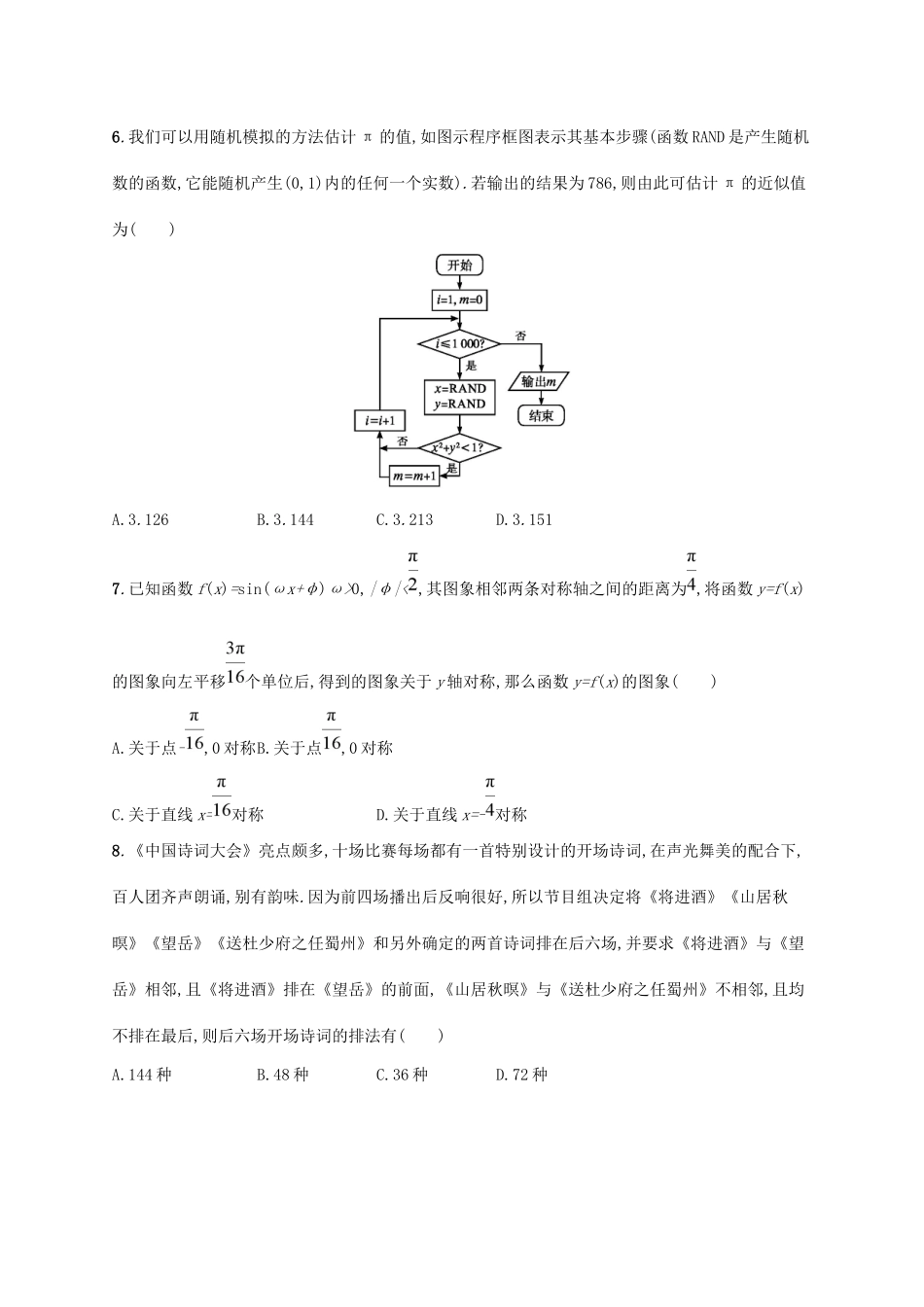
仿真模拟练(限时120分钟,满分150分)一、选择题(共12小题,每小题5分,满分60分)1.已知集合P={x∈N|1≤x≤10},集合Q={x∈R|x2-x-6<0},则P∩Q等于()A.{1,2,3}B.{1,2}C.[1,2]D.[1,3)2.若iz=-1+i,则复数z的共轭复数在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.设曲线C是双曲线,则“C的方程为x2-=1”是“C的渐近线方程为y=±2x”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.若2m>2n>1,则()A.B.lom>lonC.ln(m-n)>0D.πm-n>15.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为()A.B.C.D.6.我们可以用随机模拟的方法估计π的值,如图示程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为786,则由此可估计π的近似值为()A.3.126B.3.144C.3.213D.3.1517.已知函数f(x)=sin(ωx+φ)ω>0,|φ|<,其图象相邻两条对称轴之间的距离为,将函数y=f(x)的图象向左平移个单位后,得到的图象关于y轴对称,那么函数y=f(x)的图象()A.关于点-,0对称B.关于点,0对称C.关于直线x=对称D.关于直线x=-对称8.《中国诗词大会》亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.因为前四场播出后反响很好,所以节目组决定将《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另外确定的两首诗词排在后六场,并要求《将进酒》与《望岳》相邻,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻,且均不排在最后,则后六场开场诗词的排法有()A.144种B.48种C.36种D.72种9.已知椭圆E:=1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x-4y=0交椭圆E于A,B两点,若|AF|+|BF|=6,点M与直线l的距离不小于,则椭圆E的离心率的取值范围是()A.0,B.0,C.,1D.,110.已知变量x,y满足条件则目标函数z=的最大值为()A.B.1C.D.11.如图,在边长为2的正方形ABCD中,E,F分别为BC,CD的中点,H为EF的中点,沿AE,EF,FA将正方形折起,使B,C,D重合于点O,在构成的四面体A-OEF中,下列结论中错误的是()A.AO⊥平面EOFB.直线AH与平面EOF所成的角的正切值为2C.异面直线OH和AE所成的角为60°D.四面体A-OEF的外接球表面积为6π12.已知函数f(x)的导函数为f'(x),且对任意的实数x都有f'(x)=e-x(2x+3)-f(x)(e是自然对数的底数),且f(0)=1,若关于x的不等式f(x)-m<0的解集中恰有两个整数,则实数m的取值范围是()A.(-e,0]B.[-e2,0)C.[-e,0)D.(-e2,0]二、填空题(共4小题,每小题5分,满分20分)13.(2x+1)1-6的展开式中的常数项是.14.已知数列{an}的首项为3,等比数列{bn}满足bn=,且b1009=1,则a2018的值为.15.如图,在平面四边形ABCD中,∠A=45°,∠B=60°,∠D=150°,AB=2BC=4,则四边形ABCD的面积为.16.如图所示,将一圆的八个等分点分成相间的两组,连接每组的四个点得到两个正方形,去掉两个正方形内部的八条线段后可以形成一个正八角星.设正八角星的中心为O,并且=e1,=e2,若将点O到正八角星16个顶点的向量都写成λe1+μe2,λ,μ∈R的形式,则λ+μ的取值范围为.三、解答题(本大题共7小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(2018山东临沂三模,理17)已知等差数列{an}的n项和为Sn,a1=3,公差d>0,且a1,a3-1,a5+1成等比数列.(1)求Sn;(2)若数列{bn}的前n项和为Tn,且bn+bn+1=,求T2n.18.如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3.(1)求证:平面PAB⊥平面ABCD;(2)求二面角O-PD-C的余弦值.19.1995年联合国教科文组织宣布每年的4月23日为世界读书日,主旨宣言为“希望散居在全球各地的人们,都能享受阅读带来的乐趣,都能尊重和感谢为人类文明作出巨大贡献的文学、文化、科学思想的大师们,都能保护知识产权.”为了解大学生课外阅读情况,现从某高校随机抽取100名学生,将他们一年课外阅读量(单位:本)的数据,分成7组[20,30),[30,40),…,[80,90),并整理得到如图频率分布直方图:(1)估计其阅读量小于60本的人数;(2)已知阅读量在[20,30),[30,40),[40,50)内的学生人数比为2∶3∶5.为了解学生阅读课外书的情况,现从阅读量在[20,40)内的学生中随机...