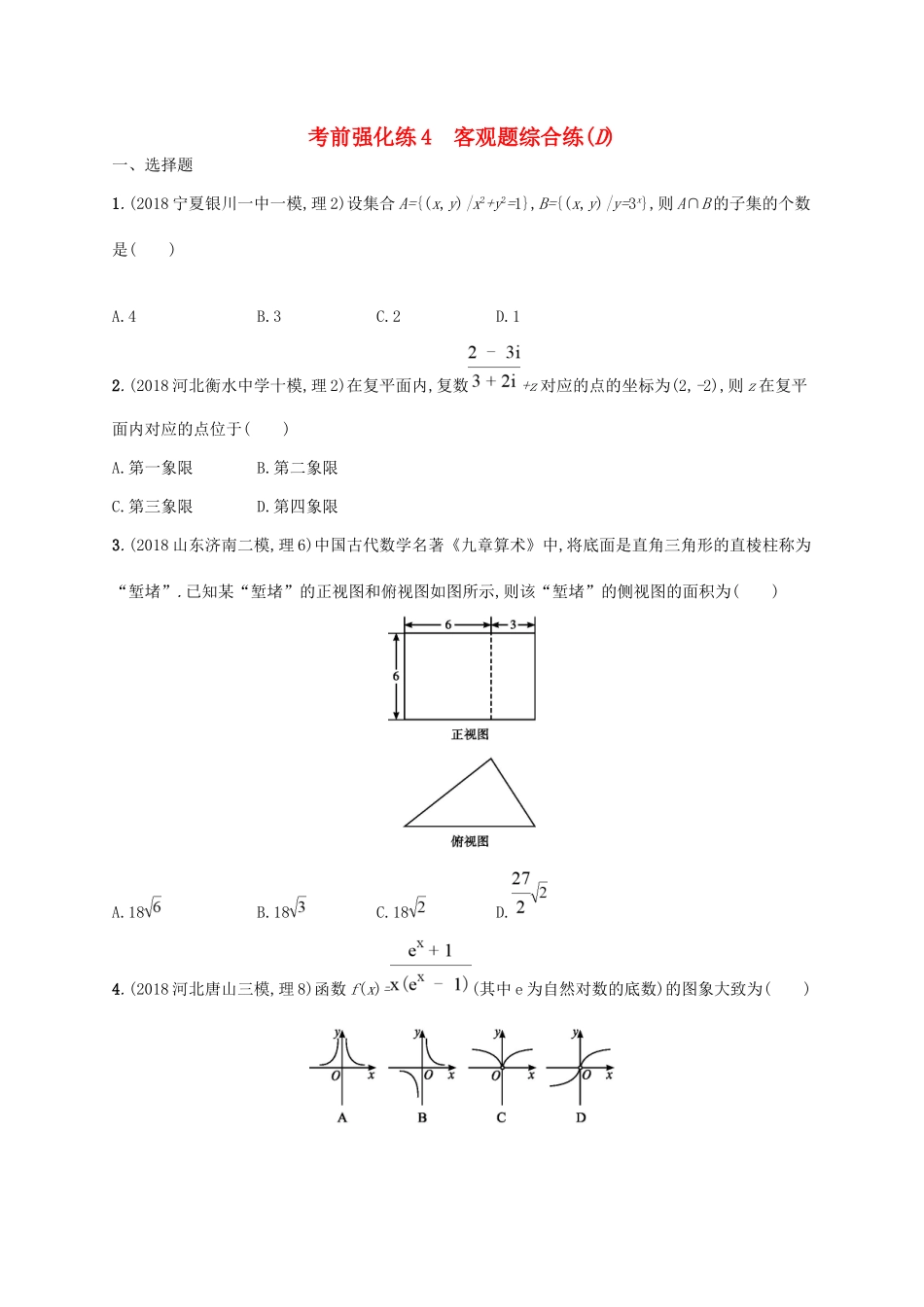
考前强化练4客观题综合练(D)一、选择题1.(2018宁夏银川一中一模,理2)设集合A={(x,y)|x2+y2=1},B={(x,y)|y=3x},则A∩B的子集的个数是()A.4B.3C.2D.12.(2018河北衡水中学十模,理2)在复平面内,复数+z对应的点的坐标为(2,-2),则z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(2018山东济南二模,理6)中国古代数学名著《九章算术》中,将底面是直角三角形的直棱柱称为“堑堵”.已知某“堑堵”的正视图和俯视图如图所示,则该“堑堵”的侧视图的面积为()A.18B.18C.18D.4.(2018河北唐山三模,理8)函数f(x)=(其中e为自然对数的底数)的图象大致为()5.若数列{an}是正项数列,且+…+=n2+n,则a1++…+等于()A.2n2+2nB.n2+2nC.2n2+nD.2(n2+2n)6.(2018河南商丘二模,理10)将函数f(x)=cos2sin-2cos+(ω>0)的图象向左平移个单位长度,得到函数y=g(x)的图象,若y=g(x)在0,上为增函数,则ω的最大值为()A.2B.4C.6D.87.(2018湖南长郡中学一模,理9)已知以原点为中心,实轴在x轴上的双曲线的一条渐近线方程为y=x,焦点到渐近线的距离为6,则此双曲线的标准方程为()A.=1B.=1C.=1D.=18.(2018河南六市联考一,文11)如图是计算函数y=的值的程序框图,则在①②③处应分别填入的是()A.y=-x,y=0,y=x2B.y=-x,y=x2,y=0C.y=0,y=x2,y=-xD.y=0,y=-x,y=x29.设等差数列{an}的前n项和为Sn,已知a1=9,a2为整数,且Sn≤S5,则数列的前9项和为()A.-B.-C.-9D.810.(2018山东潍坊一模,理9)已知函数f(x)=2sin(ωx+φ)φ>0,|φ|<的最小正周期为4π,其图象关于直线x=π对称.给出下面四个结论:①函数f(x)在区间0,π上先增后减;②将函数f(x)的图象向右平移个单位后得到的图象关于原点对称;③点-,0是函数f(x)图象的一个对称中心;④函数f(x)在[π,2π]上的最大值为1.其中正确的是()A.①②B.③④C.①③D.②④11.抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线=1(a>0,b>0)的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为()A.B.2C.D.+112.若关于x的方程+m=0有3个不相等的实数解x1,x2,x3,且x1<00且增大时,f(x)的值减小,故选A.5.A解析+…+=n2+n,∴n=1时,=2,解得a1=4.n≥2时,+…+=(n-1)2+n-1,相减可得=2n,∴an=4n2.n=1时也满足=4n.则a1++…+=4(1+2+…+n)=4=2n2+2n.故选A.6.C解析f(x)=cos2sin-2cos+=sinωx-2=sinωx-cosωx=2sinωx-,f(x)的图象向左平移个单位长度,得y=2sinωx+-的图象,∴函数y=g(x)=2sinωx.又y=g(x)在0,上为增函数,,即,解得ω≤6,所以ω的最大值为6.7.C解析 双曲线的一条渐近线方程是y=x,=6,∴c=10. c2=a2+b2,∴a2=64,b2=36.∴双曲线方程为=1,故选C.8.B解析由题意及框图可知,在①应填“y=-x”;在②应填“y=x2”;在③应填“y=0”.9.A解析由题意Sn=n2+a1-n=n2+9-n,d<0,d∈Z,对称轴n=,当d=-1时,对称轴n=,不满足Sn≤S5,若d=-2,对称轴n=5满足题意,∴d=-2,an=a1+(n-1)×(-2)=11-...