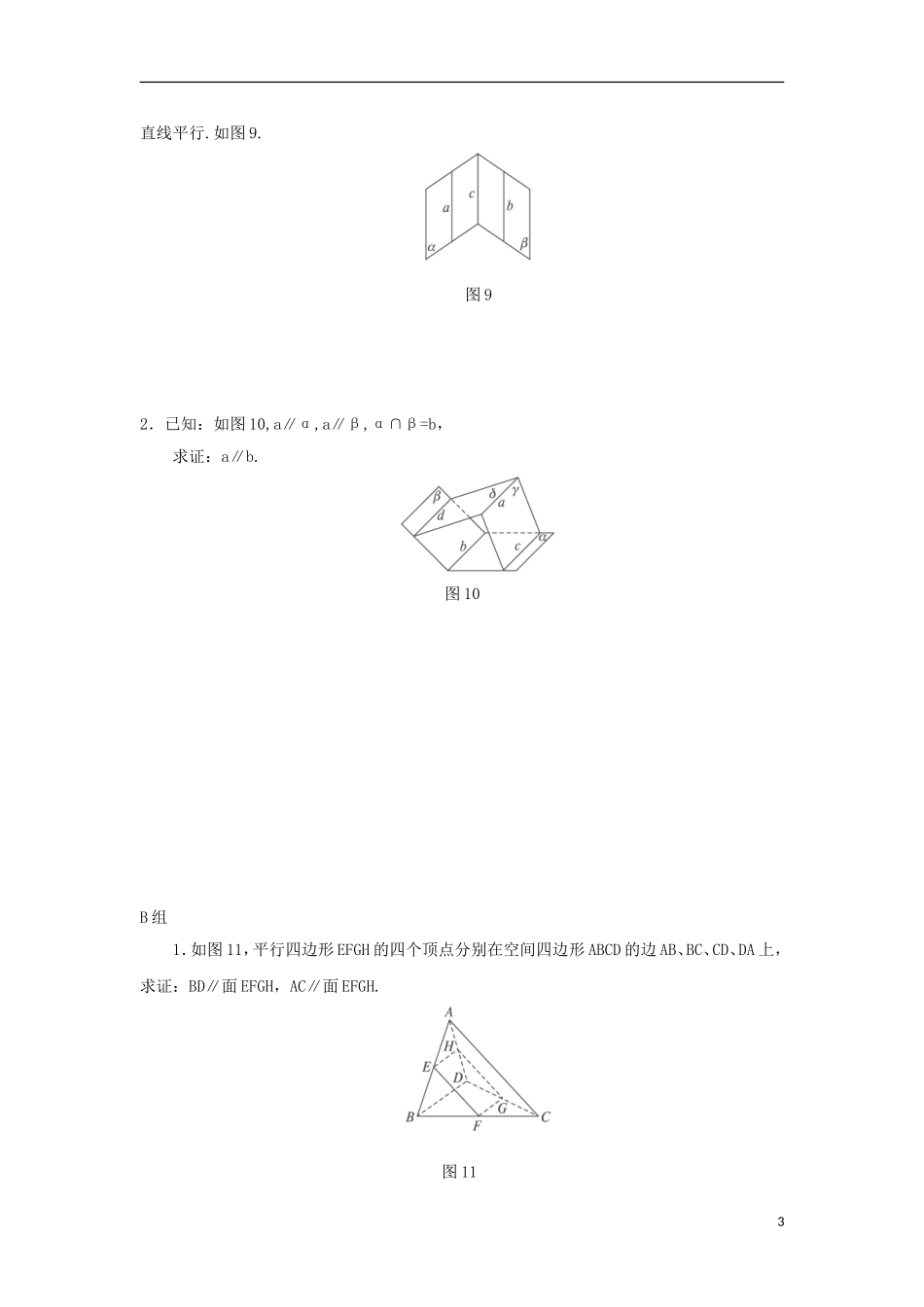
云南省德宏州潞西市芒市中学 2014 年高中数学 2.2.3 直线与平面平行的性质学案 新人教 A 必修 2一、学习目标(1)探究直线与平面平行的性质定理.(2)体会直线与平面平行的性质定理的应用.(3)通过线线平行与线面平行转化,培养学习兴趣.二、问题与例题问题 1 教室内日光灯管所在的直线与地面平行,是不是地面内的所有直线都与日光灯管所在的直线平行?问题 2 那么灯管和地面内的哪些直线平行?怎样画出它?问题 3 你能证明直线与平面平行的性质定理吗?问题 4 应用线面平行的性质定理的关键是什么?例 1 如图 4 所示的一块木料中,棱 BC 平行于面 A′C′.图 4(1)要经过面 A′C′内的一点 P 和棱 BC 将木料锯开,应怎样画线?(2)所画的线与面AC 是什么位置关系?例 2 已知平面外的两条平行直线中的一条平行于这个平面,求证另一条也平行于这个平面.如图 7.图 7三、目标检测1.如图 6,a∥α,A 是 α 另一侧的点,B、C、D∈a,线段 AB、AC、AD 交 α 于 E、F、G 点,若BD=4,CF=4,AF=5,求 EG.1图 62.如图 8,E、H 分别是空间四边形 ABCD 的边 AB、AD 的中点,平面 α 过 EH 分别交 BC、CD于 F、G.求证:EH∥FG.图 8四、配餐作业A 组1. 求证:如果两个相交平面分别经过两条平行直线中的一条,那么它们的交线和这条2直线平行.如图 9.图 92.已知:如图 10,a∥α,a∥β,α∩β=b,求证:a∥b.图 10B 组1.如图 11,平行四边形 EFGH 的四个顶点分别在空间四边形 ABCD 的边 AB、BC、CD、DA 上,求证:BD∥面 EFGH,AC∥面 EFGH.图 113C 组1. 如图12,平面 EFGH 分别平行于 CD、AB,E、F、G、H 分别在 BD、BC、AC、AD 上,且CD=a,AB=b,CD⊥AB.图 12(1)求证:EFGH 是矩形;(2)设 DE=m,EB=n,求矩形 EFGH 的面积.4