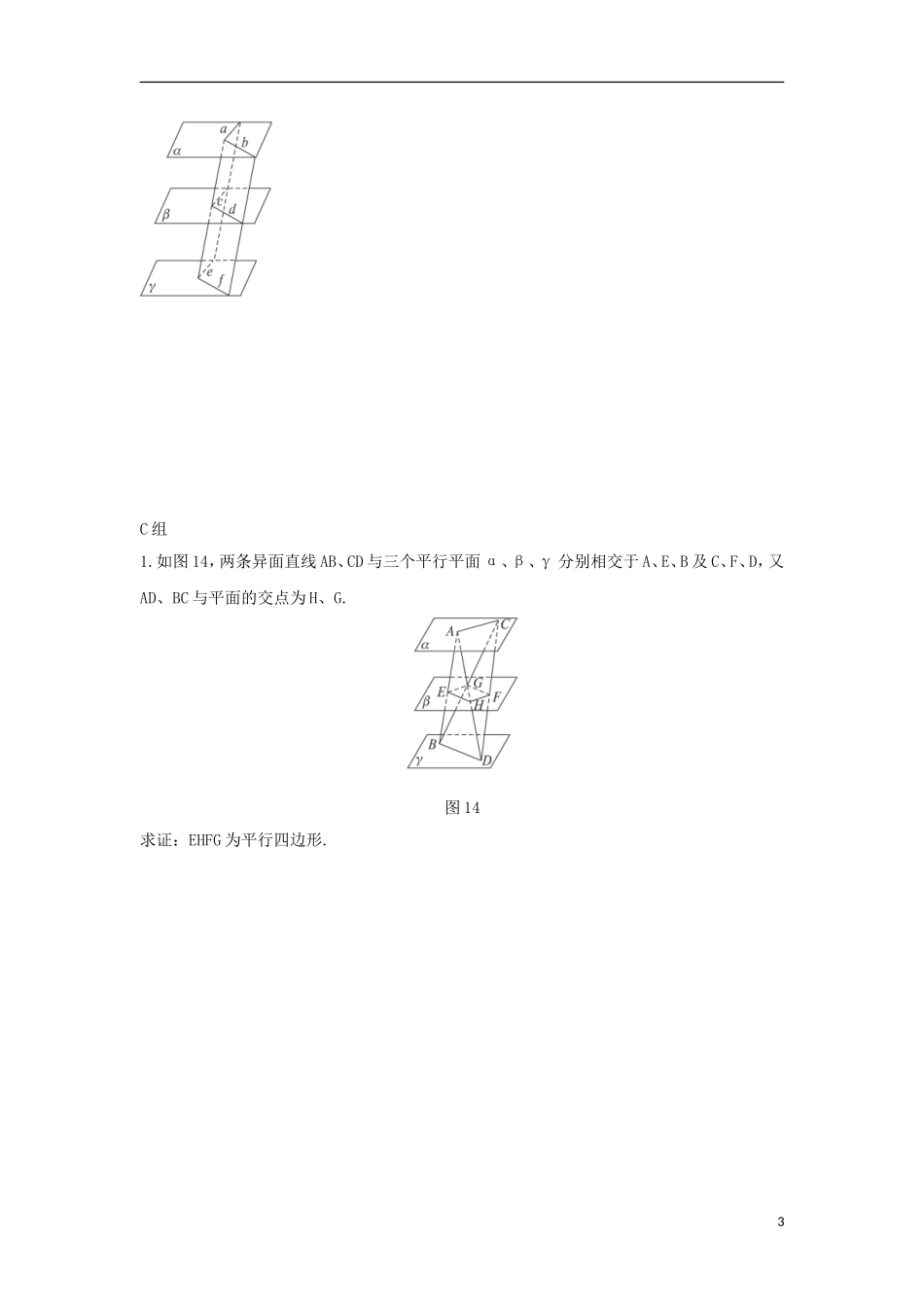
云南省德宏州潞西市芒市中学 2014 年高中数学 2.2.4 平面与平面平行的性质教学案 新人教 A 版必修 2一、学习目标(1)通过图形探究平面与平面平行的判定定理及其性质定理;(2)熟练掌握平面与平面平行的判定定理和性质定理的应用;(3)进一步培养空间想象能力,以及逻辑思维能力;二、问题与例题1.创设情景,导入新课三角板的一条边所在直线与桌面平行,这个三角板所在的平面与桌面平行吗?三角板的两条边所在直线分别与桌面平行,情况又如何呢?2.新知探究问题 1 要证线面平行可转化为线线平行,欲判定面面平行可如何转化?问题 2 怎样用三种语言描述平面与平面平行的判定定理?问题 3 应用面面平行的判定定理应注意什么? 问题 4 利用空间模型探究:如果两个平面平行,那么一个平面内的直线与另一个平面内的直线具有什么位置关系?问题 5 回忆线面平行的性质定理,结合模型探究面面平行的性质定理是什么?问题 6 试用三种语言描述平面与平面平行的性质定理。问题 7 应用面面平行的性质定理的难点在哪里?问题 8 应用面面平行的性质定理口诀是什么?3.例题课本例 5、例 6 4.目标检测(1)例 1 已知正方体 ABCD—A1B1C1D1,如图 9,求证:平面 AB1D1∥平面 BDC1.图 91 (2)如图 11,已知平面 α、β、γ 满足 α∥β,α∩γ=a,β∩γ=b,求证:a∥b.图 11 三、配餐作业A 组1.如图 10,在正方体 ABCD—EFGH 中,M、N、P、Q、R 分别是 EH、EF、BC、CD、AD 的中点,求证:平面 MNA∥平面 PQG.。图 10 B 组2.如果两个平面分别平行于第三个平面,那么这两个平面互相平行。2 C 组1.如图 14,两条异面直线 AB、CD 与三个平行平面 α、β、γ 分别相交于 A、E、B 及 C、F、D,又AD、BC 与平面的交点为 H、G.图 14求证:EHFG 为平行四边形.3