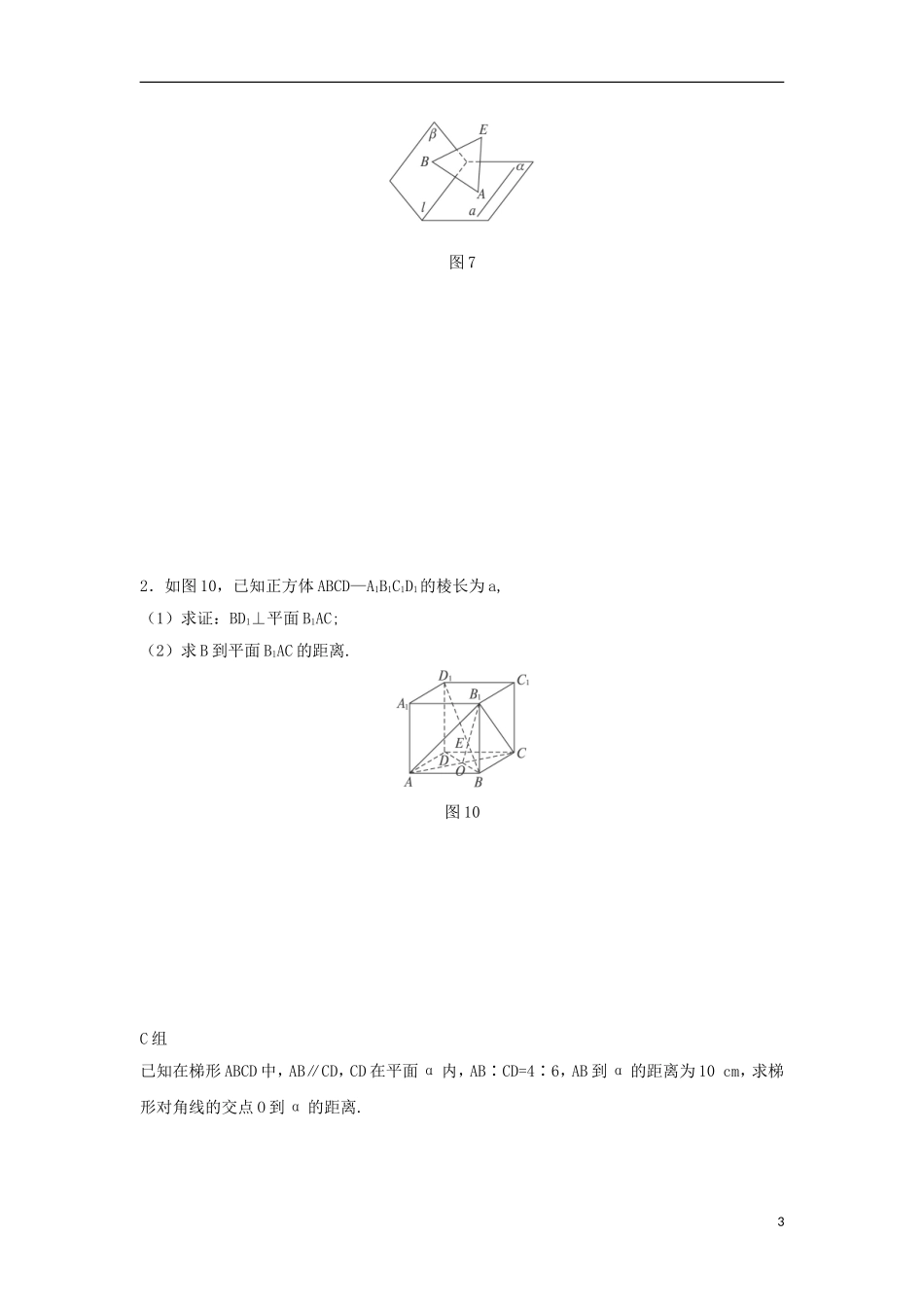
云南省德宏州潞西市芒市中学 2014 年高中数学 2.3.3 直线与平面垂直的性质教学案(1)新人教 A 版必修 2一、学习目标1.探究直线与平面垂直的性质定理,培养空间想象能力、实事求是等严肃的科学态度和品质;2.掌握直线与平面垂直的性质定理的应用提高逻辑推理的能力.二、问题与例题1.创设情景,导入新课三角板的一条边所在直线与桌面平行,这个三角板所在的平面与桌面平行吗?三角板的两条边所在直线分别与桌面平行,情况又如何呢?2.新知探究问题 1 怎样定义空间两直线平行?问题 2 同垂直于一条直线的两条直线的位置关系如何? 问题 3 找出恰当空间模型探究同垂直于一个平面的两条直线的位置关系。问题 4 用三种语言描述直线与平面垂直的性质定理。问题 5 如何理解直线与平面垂直的性质定理的地位与作用?3.例题例 1 证明垂直于同一个平面的两条直线平行.解:已知 a⊥α,b⊥α.求证:a∥b.图 6证明:(反证法)如图 6,假定 a 与 b 不平行,且 b∩α=O,作直线 b′,使 O∈b′,a∥b′.直线 b′与直线 b 确定平面 β,设 α∩β=c,则 O∈c.∵a⊥α,b⊥α,∴a⊥c,b⊥c.∵b′∥a,∴b′⊥c.又∵O∈b,O∈b′,bβ,b′β,a∥b′显然不可能,因此 b∥a.4.目标检测[来源:]如图 8,已知直线 a⊥b,b⊥α,aα.求证:a∥α.1图 8三、配餐作业A 组1.已知 a、b、c 是平面 α 内相交于一点 O 的三条直线,而直线 l 和平面 α 相交,并且和a、b、c 三条直线成等角.求证:l⊥α.2.如图 9,已知 PA⊥矩形 ABCD 所在平面,M、N 分别是 AB、PC 的中点.(1)求证:MN⊥CD;(2)若∠PDA=45°,求证:MN⊥面 PCD.图 9B 组1.如图 7,已知 α∩β=l,EA⊥α 于点 A,EB⊥β 于点 B,aα,a⊥AB.求证:a∥l.2 图 72.如图 10,已知正方体 ABCD—A1B1C1D1的棱长为 a,(1)求证:BD1⊥平面 B1AC;(2)求 B 到平面 B1AC 的距离.图 10 C 组已知在梯形 ABCD 中,AB∥CD,CD 在平面 α 内,AB∶CD=4∶6,AB 到 α 的距离为 10 cm,求梯形对角线的交点 O 到 α 的距离.3图 114