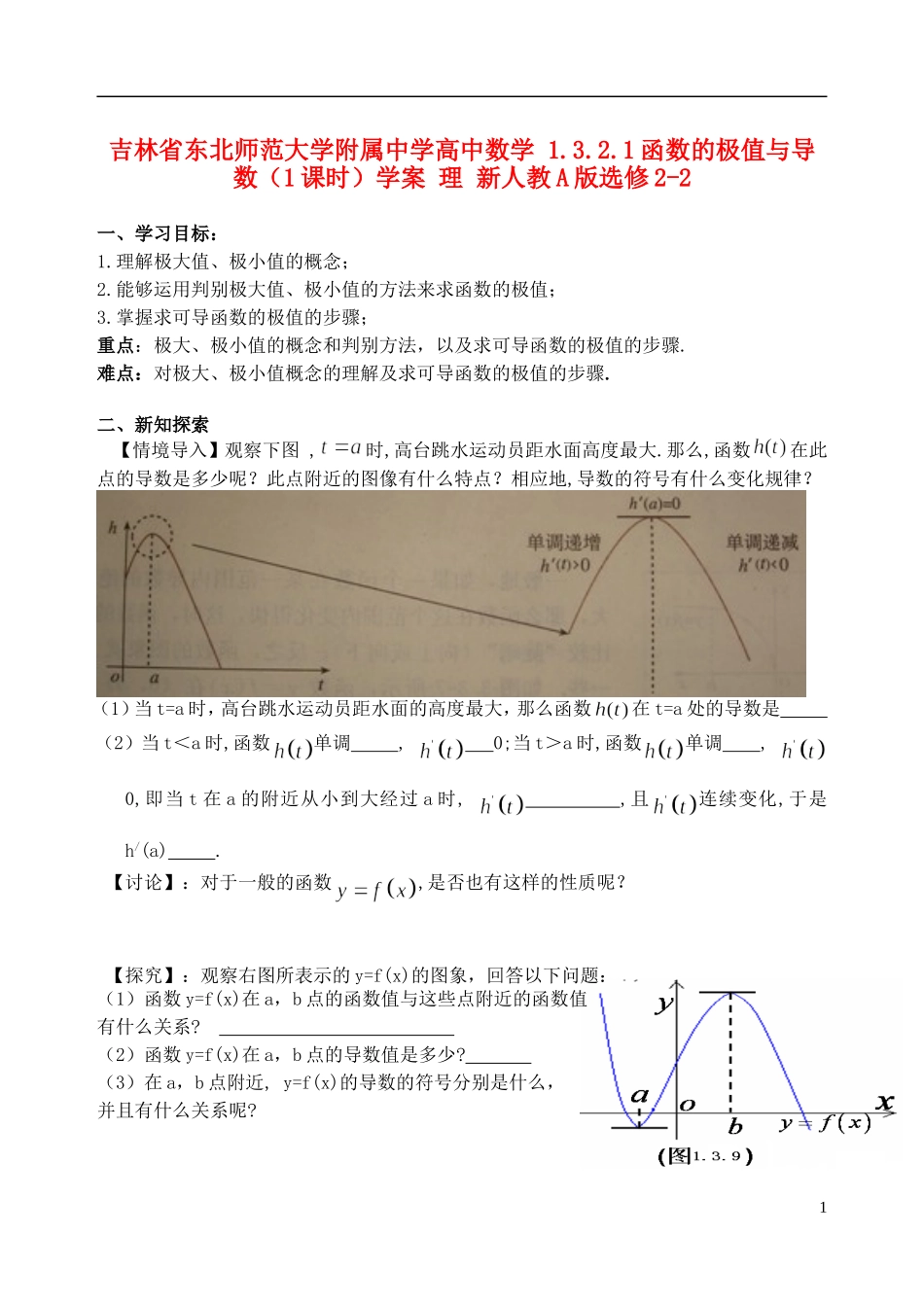
吉林省东北师范大学附属中学高中数学 1.3.2.1 函数的极值与导数(1 课时)学案 理 新人教 A 版选修 2-2一、学习目标:1.理解极大值、极小值的概念;2.能够运用判别极大值、极小值的方法来求函数的极值;3.掌握求可导函数的极值的步骤;重点:极大、极小值的概念和判别方法,以及求可导函数的极值的步骤.难点:对极大、极小值概念的理解及求可导函数的极值的步骤.二、新知探索【情境导入】观察下图 ,时,高台跳水运动员距水面高度最大.那么,函数在此点的导数是多少呢?此点附近的图像有什么特点?相应地,导数的符号有什么变化规律?(1)当 t=a 时,高台跳水运动员距水面的高度最大,那么函数在 t=a 处的导数是 (2)当 t<a 时,函数单调 , 0;当 t>a 时,函数单调 , 0,即当 t 在 a 的附近从小到大经过 a 时, ,且连续变化,于是h/(a) .【讨论】:对于一般的函数,是否也有这样的性质呢? 【探究】:观察右图所表示的 y=f(x)的图象,回答以下问题:(1)函数 y=f(x)在 a,b 点的函数值与这些点附近的函数值有什么关系? (2)函数 y=f(x)在 a,b 点的导数值是多少? (3)在 a,b 点附近, y=f(x)的导数的符号分别是什么,并且有什么关系呢?1 【新知】极值的定义:我们把点 a 叫做函数 y=f(x)的 ,f(a)叫做函数 y=f(x)的 ;点 b 叫做函数 y=f(x)的 ,f(b)叫做函数 y=f(x)的 。极大值点与极小值点称为 , 极大值与极小值称为极值.通过以上探索,你能归纳出可导函数在某点 x0取得极值的充要条件吗? 【练习】观察图 1.3.10,回答以下问题:(1)找出图中的极点,并说明哪些点为极大值点,哪些点为极小值点?(2)极大值一定大于极小值吗?四、例题精析例 1 求函数的极值 变式:1、求函数的极值 2、已知函数在处取得极值,求函数解析式及单调区间。六、小结21、函数极值的定义;2、函数极值求解步骤 3、一个点为函数的极值点的充要条件。七、日日清1.“函数 y=f(x)在一点的导数值为 0”是“函数 y=f(x)在这点取极值”的( )A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件2.函数 f(x)=x3+ax2+3x-9,已知 f(x)在 x=-3 时取得极值,则 a=( )A.2 B.3 C.4 D.53.下列函数存在极值的是( )A.y= B.y=x-ex C.y=x3+x2+2x-3 D.y=x34.函数 f(x)的定义域为开区间(a,b),导函数 f′(x)在(a,b)内的图象如图所示,则函数f(x)在...