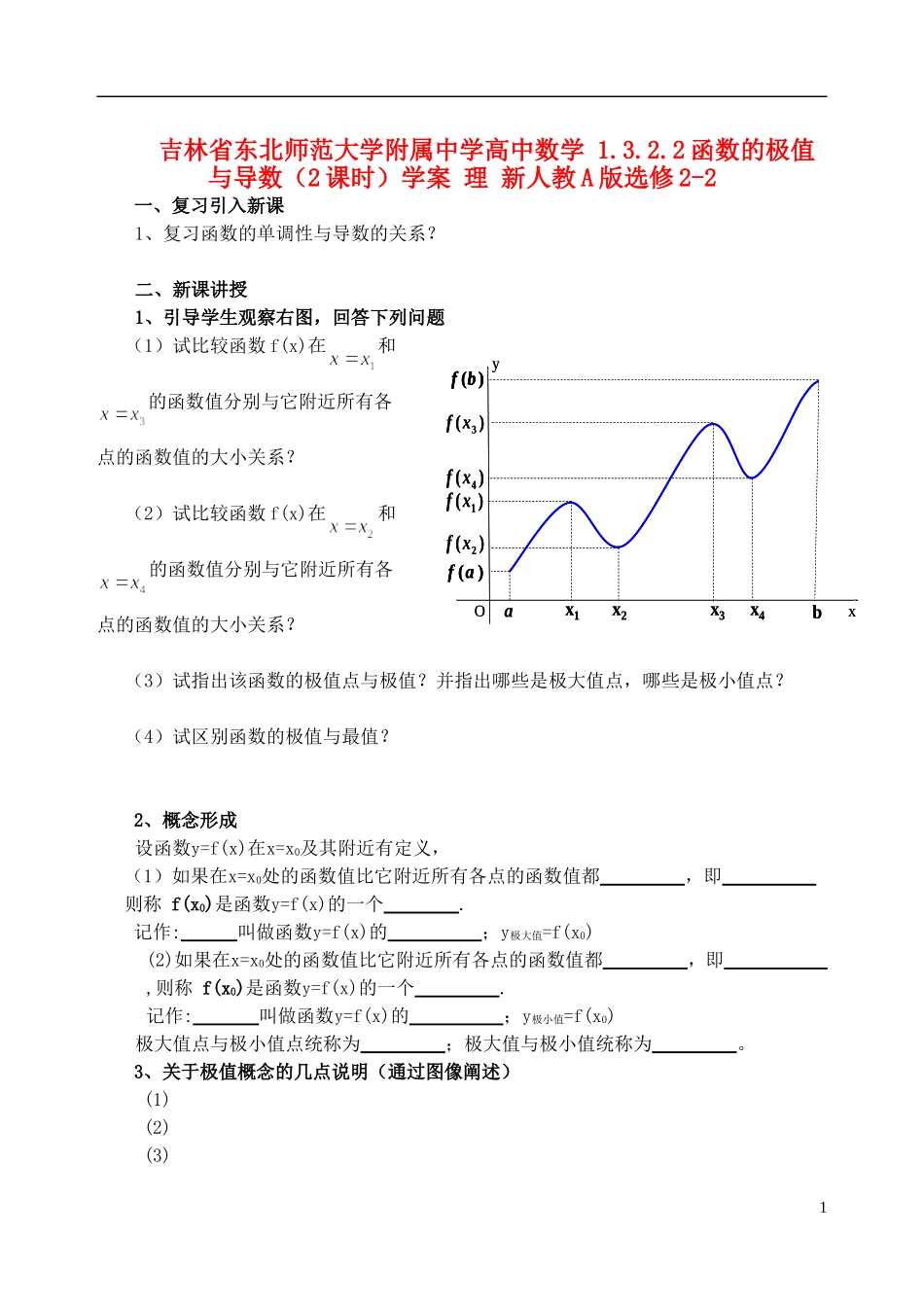
吉林省东北师范大学附属中学高中数学 1.3.2.2 函数的极值与导数(2 课时)学案 理 新人教 A 版选修 2-2一、复习引入新课1、复习函数的单调性与导数的关系? 二、新课讲授1、引导学生观察右图,回答下列问题(1)试比较函数 f(x)在和的函数值分别与它附近所有各点的函数值的大小关系?(2)试比较函数 f(x)在和的函数值分别与它附近所有各点的函数值的大小关系?(3)试指出该函数的极值点与极值?并指出哪些是极大值点,哪些是极小值点?(4)试区别函数的极值与最值?2、概念形成 设函数y=f(x)在x=x0及其附近有定义,(1)如果在x=x0处的函数值比它附近所有各点的函数值都 ,即 则称 f(x0)是函数y=f(x)的一个 . 记作: 叫做函数y=f(x)的 ;y极大值=f(x0)(2)如果在x=x0处的函数值比它附近所有各点的函数值都 ,即 ,则称 f(x0)是函数y=f(x)的一个 . 记作: 叫做函数y=f(x)的 ;y极小值=f(x0)极大值点与极小值点统称为 ;极大值与极小值统称为 。3、关于极值概念的几点说明(通过图像阐述) (1) (2)(3) 1ybx1x2x3x4)(1xf)(4xfOx)(2xf)(3xf)(afa)(bfybx1x2x3x4)(1xf)(4xfOx)(2xf)(3xf)(af)(afa)(bf)(bf(4) 4、函数的极值与导数的关系(1)如果f /(x0)=0,, 并且在x0附近的左侧 ;右侧 , 那么f(x0)是 ( )(2)如果f /(x0)=0, 并且在x0附近的左侧 ;右侧 , 那么f(x0)是 ( )归纳:对可导函数,x= x0为极值点的充要条件是: 。 5、辨析:导数值为0的点一定是函数的极值点吗? 对可导函数,导数值为0的点是该点为极值点的 。三、例题精解例1:(1)下图是导函数f /(x)的图象, 试找出函数f (x)的极值点, 并指出哪些是极大值点, 哪些是极小值点?例2: 求函数 的极值 (略)求函数极值的基本步骤(引导学生归纳)(1)(2)(3)(4)2四、练习1、求下列函数的极值: 3