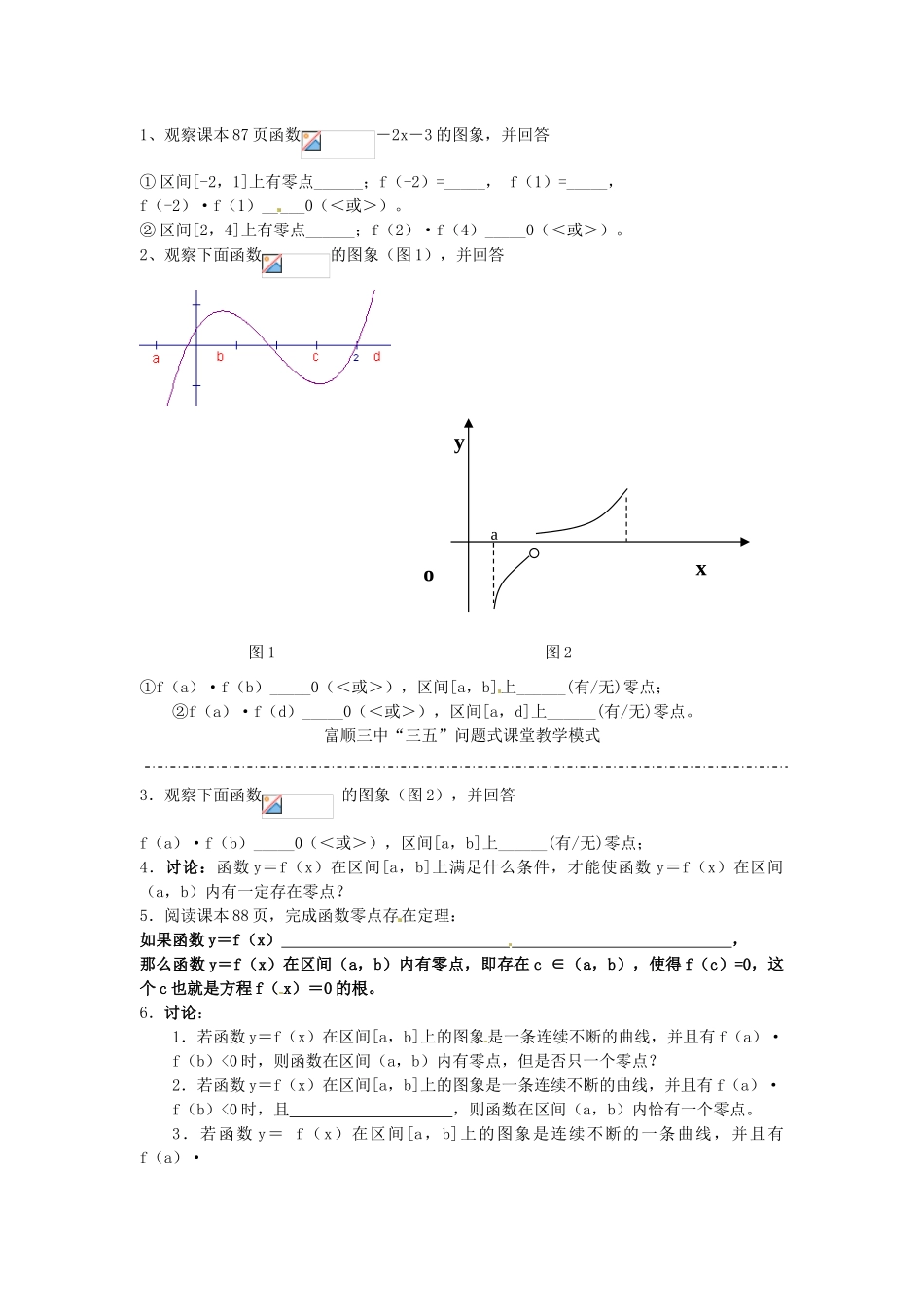
四川省富顺县第三中学高一数学学案:3.1.1 方程的根与函数的零点【学习目标】(1)了解函数的零点与方程根的联系。(2)理解并会应用函数在某区间上存在零点的判定。(3)在探究过程中体验发现的乐趣,体会数形结合,函数与方程以及转化的数学思想。【重点难点】了解函数的零点与方程的根之间的联系,掌握求函数零点的方法和零点存在的判定条件。探究发现函数零点的存在的判定条件。【导学过程】自主学习1、求方程的根并画出对应函数的图像。① 方程 x-6=0 与函数 y=x-6② 方程与函数③ 方程与函数④ 方程与函数2、交流、讨论,总结方程的根与对应函数图像间的关系:方程有几个根,对应函数的图像与 x 轴___________,且方程的根就是图像与 x 轴____________。 3、零点概念:对于函数,我们把使___________________________叫做函数的零点。合作探究一、函数零点1、是不是所有的二次函数都有零点?最多有几个零点?完成下表。判别式△>0△=0△<0的根有两个相等的实数根的图像的零点2、 试说说方程的根、函数的图像与 x 轴的交点、函数的零点的关系,并归纳总结。⑴ 零点是对于________而言,不是相对于________而言。⑵ 函数零点的意义:函数的零点就是方程___________,即函数的图像与_______________。⑶ 方程________ 函数___________________函数___________。⑷ 函数的零点并不是“____”,它不是以坐标的形式出现的,而是________。例如,函数的零点为 x=-1 和 3。口诀:零点不是“点“,截距不是“距”。2、 想一想,如何根据函数零点的意义求零点?可以(代数法)_____________________________________________________;也可以 (几何法)_____________________________________________________。4、练一练:求下列函数的零点:⑴⑵⑶ 如何判断函数有没有零点?二、函数零点存在定理1、观察课本 87 页函数-2x-3 的图象,并回答① 区间[-2,1]上有零点______;f(-2)=_____, f(1)=_____,f(-2)·f(1)_____0(<或>)。② 区间[2,4]上有零点______;f(2)·f(4)_____0(<或>)。2、观察下面函数的图象(图 1),并回答 图 1 图 2①f(a)·f(b)_____0(<或>),区间[a,b]上______(有/无)零点; ②f(a)·f(d)_____0(<或>),区间[a,d]上______(有/无)零点。富顺三中“三五”问题式课堂教学模式3.观察下面函数 的图象(图 2),并回答f(a)·f(b)_____0(<或>...