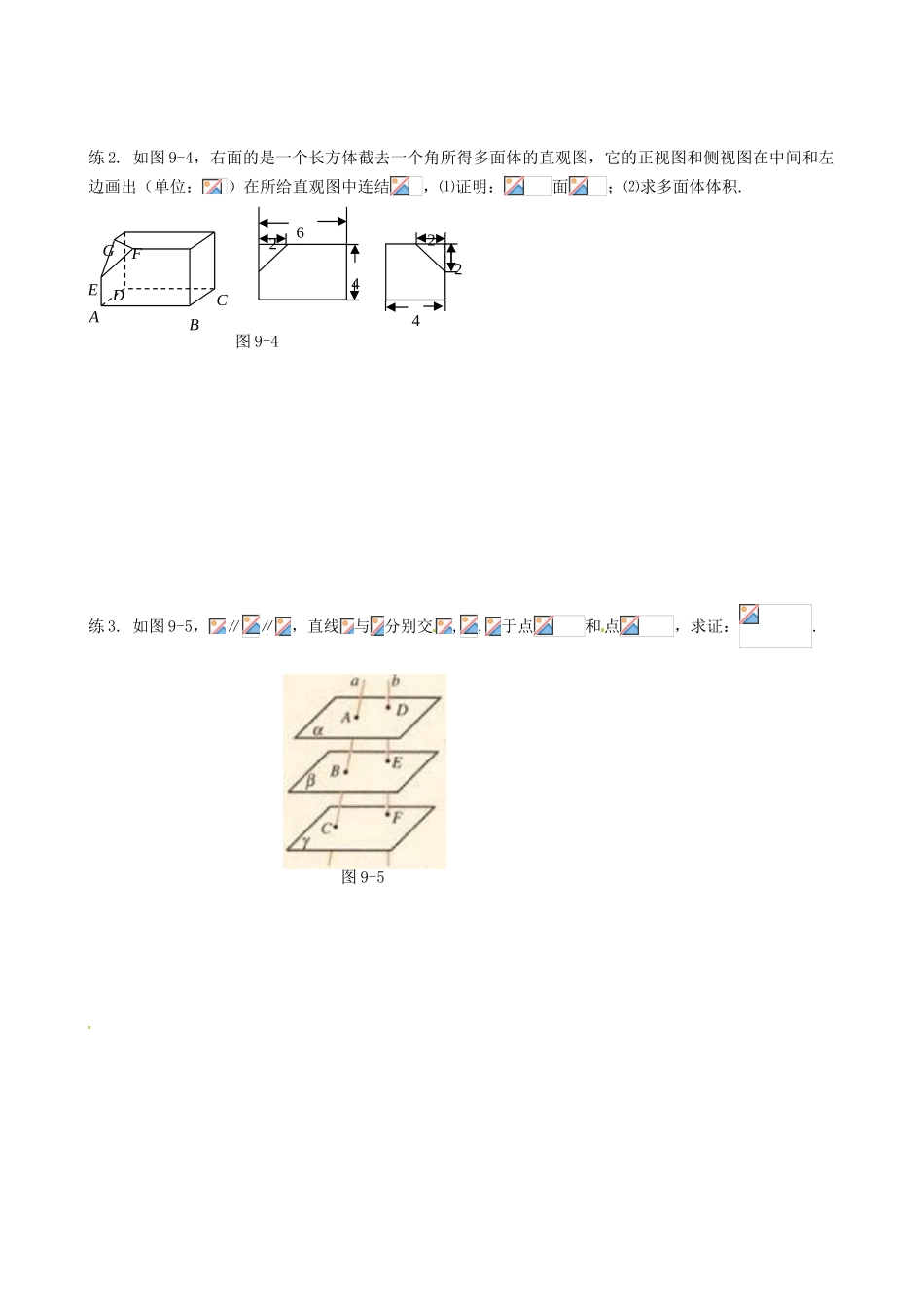
§2.2 直线、平面平行的判定及其性质(练习)学习目标:1. 熟练掌握直线与平面、平面与平面平行的判定定理和性质定理,能合理选用其证明平行关系;2. 熟练掌握线线、线面、面面之间的相互转化关系..课前预习(预习教材 P54~ P63,找出疑惑之处)复习 1:直线与平面、平面与平面平行的判定定理和性质定理分别是什么?复习 2:线线平行、线面平行、面面平行相互之间的转化图为:线线平行 线面平行面面平行 课内探究例 1 如图 9-1,在正方体中,分别为,的中点.求证:⑴∥;⑵∥;⑶∥.图 9-1 判定定理性质定理例 2 如图 9-2,在四棱锥中,底面是菱形,为的中点,为的中点,证明:直线图 9-2小结:判断某一平行的过程就是从一平行关系出发不断转化的过程.通常经历线线平行到线面平行,线面平行到面面平行,最后又回到线线平行这一过程,归根结底还是线线平行.※ 动手试试练 1. 如图 9-3,直线相交于点,=,,,求证:平面∥平面.图 9-3练 2. 如图 9-4,右面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在中间和左边画出(单位:)在所给直观图中连结,⑴证明:面;⑵求多面体体积.图 9-4练 3. 如图 9-5,∥∥,直线与分别交,,于点和点,求证:.图 9-546422EDABCFG2当堂检测1. 下列条件能推出平面∥平面的是( ). A.存在一条直线,∥,∥ B.存在一条直线,,∥ C.存在两条平行直线,,∥,∥ D. 存在两条异面直线,,∥,∥2. 设为两条直线,为两个平面,下列三个结论正确的有( )个.① 若与所成的角相等,则∥② 若∥,∥,∥,则∥③ 若,∥,则∥ A.0 B.1 C.2 D.33. 和是夹在平行平面间的两条异面线段,分别是它们的中点,则和( ). A.平行 B.相交 C.垂直 D.不能确定4. 在由正方体棱的中点组成的直线中,和正方体的一个对角面平行的直线有_______条.5. ,试在横线上写出条件,使得∥.____________________________________课后反思线面平行、面面平行判定定理和性质定理的熟练运用;平行关系的熟练转化. 知识拓展 在立体几何中,证明图形的存在性或唯一性时,常常运用反证法和同一法.反证法:先提出和原命题中的结论相反的假定,然后从这个假定中得出和已知条件相矛盾的结果 ,这样就否定了原来的假定而肯定原命题.同一法:欲证图形 有某种特性时,可另作一个具有同样特征的图形,再证明所作图形和已知条件中的图形是同一个.如果不是同一个,则与某公理或定理相矛盾.课后训练1. 如图 9-6,四边形是矩形,是、的中点,求证:∥面.图 9-62. 如图 9-7,在正三棱柱中,是的中点,求证:∥面.