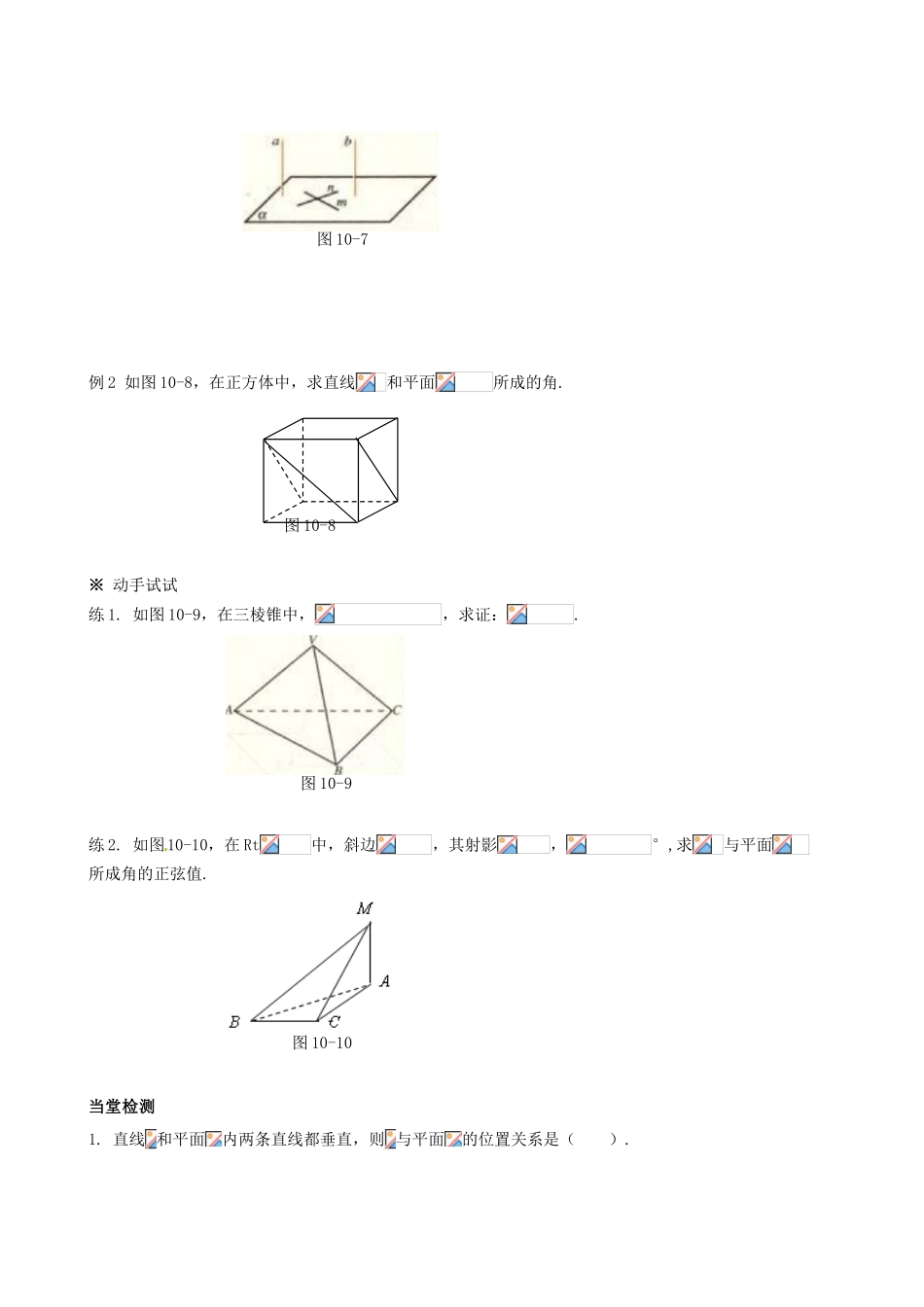
§2.3.1 直线与平面垂直的判定学习目标:1. 理解直线与平面垂直的定义;2. 掌握直线与平面垂直的判定定理及其应用;3. 理解直线与平面所成的角的概念,会求直线与平面所成的角.学习重点: 操作确认并概括出直线与平面垂直的定义和判定定理。学习难点: 操作确认并概括出直线与平面垂直的判定定理及初步运用课前预习(预习教材 P64~ P67,找出疑惑之处)复习 1:当两条直线的夹角为______,这两条直线互相垂直;它们的位置关系是_______或________.复习 2:如图 10-1,直线,请你任意作出至少 3 条和垂直的直线,并感觉作出的直线中有和平面垂直的直线吗?图 10-1课内探究探究 1:直线和平面垂直的概念问题:如图 10-2,将三角板直立起来,并且让它的一条直角边落在桌面上,观察边与桌面的位置关系呈什么状态?绕着边转动三角板,边与始终垂直吗?在转动的过程中,把看作桌面上不同的直线,你能得出什么结论吗?图 10-2新知 1:如果直线 与平面内的任意一条直线都垂直,就说直线 与平面互相垂直,记做. 叫做垂线,叫垂面,它们的交点叫垂足.如图 10-3 所示.图 10-3反思:⑴如果直线与平面内无数条直线都垂直,那么它和这个平面垂直吗?⑵用定义证明直线和平面垂直好证吗?你感觉难在哪里?探究 2:直线与平面垂直的判定定理问题:如图 10-4,将一块三角形纸片沿折痕折起,将翻折后的纸片竖起放置在桌面上(与桌面接触).观察折痕与桌面的位置关系.如何翻折才能使折痕与桌面垂直呢?图 10-4结论:当且仅当折痕是边上的高时,所在的直线与桌面所在的平面垂直.如下图所示. 图 10-5反思:⑴折痕与桌面上的一条直线垂直时,能判断垂直于桌面吗?⑵ 如图 10-5,当折痕时,翻折后,即.由此你能得出什么结论?新知 2:直线和平面垂直的判定定理 一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.探究 3:直线与平面所成的角新知 3:如图 10-6,直线和平面相交但不垂直,叫做平面的斜线,和平面的交点叫斜足;,叫做斜线在平面上的射影.平面的一条斜线和它在平面上的射影所成的锐角,叫这条直线和平面所成的角.图 10-6直线垂直于平面,则它们所成的角是直角;直线和平面平行或在平面内,则它们所成的角是°角. 例 1 如图 10-7,已知∥,,求证:.图 10-7例 2 如图 10-8,在正方体中,求直线和平面所成的角.图 10-8※ 动手试试练 1. 如图 10-9,在三棱锥中,,求证:.图 10-9练 2. 如图10-10,...