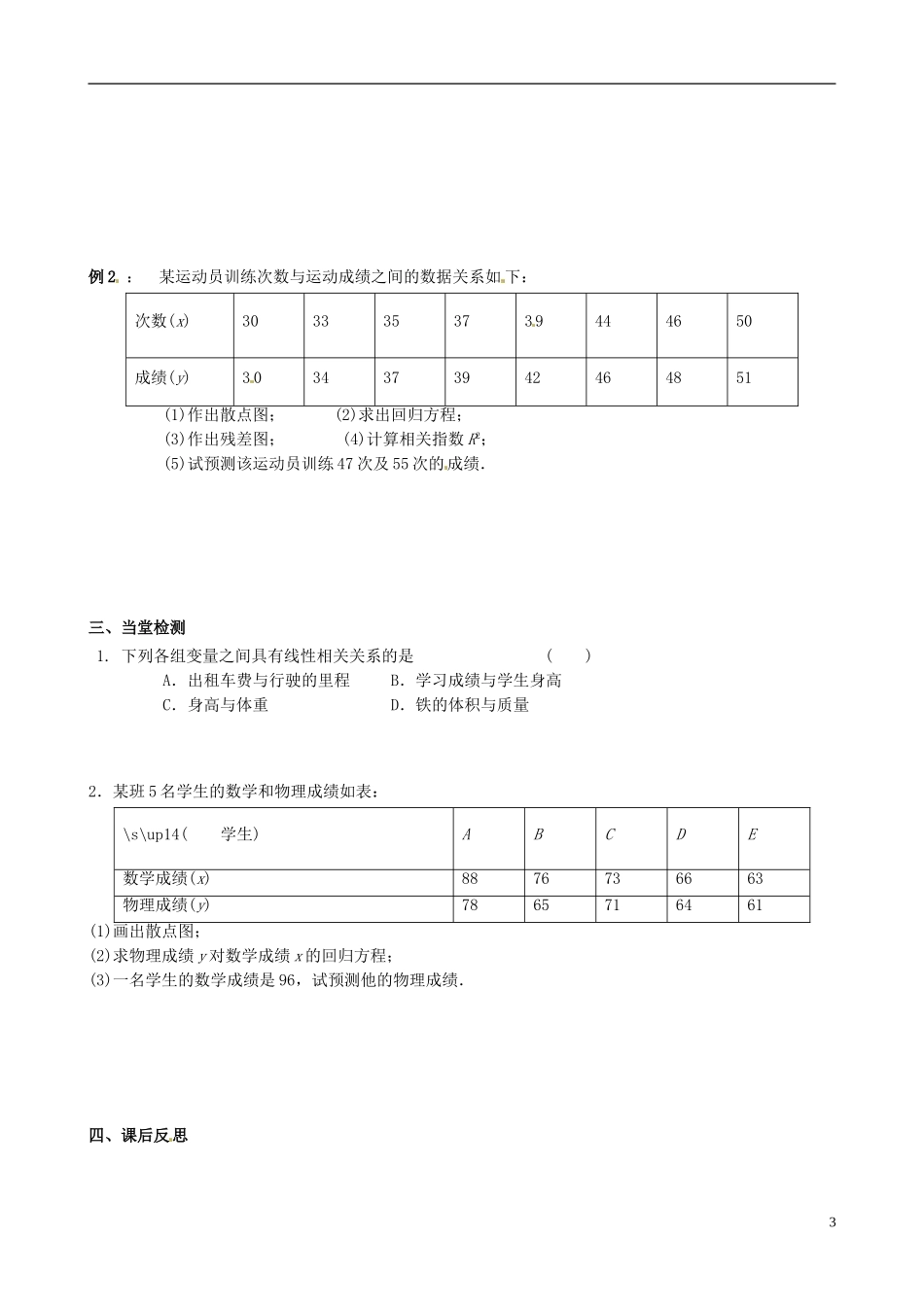
§3.1.1 回归分析的基本思想及其初步运用学习目标 :1.了解随机误差、残差、残差图的概念.2.会通过分析残差判断线性回归模型的拟合效果.3.掌握建立线性回归模型的步骤.学习重点:掌握建立线性回归模型的步骤.学习难点:掌握建立线性回归模型的步骤.课前预习案教材助读:阅读教材的内容,思考并完成下列问题:1.线性回归模型(1)函数关系是一种 关系,而相关关系是一种 关系.(2)回归分析是对具有 关系的两个变量进行统计分析的一种常用方法.(3)对于一组具有线性相关关系的数据(x1,y1),(x2,y2),…,(xn,yn),回归直线的斜率和截距的最小二乘估计公式分别为b= =,a = ,其中 称为样本点的中心.(4)线性回归模型 y=bx+a+e,其中 a 和 b 是模型的未知参 数,e 称为 ,自变量 x 称为 ,因变量 y 称为 .2.残差的概念对于样本点(x1,y1),(x2,y2),…,(xn,yn)而言,它们的随机误差为 ei= ,i=1,2,…,n,其估计值为e i= = ,i=1,2,…,n,e i称为相应于点(xi,yi)的 .3.刻画回归效果的方式(1)残差图法作图时 为残差, 可以选为的样本编号,或身高数据,或体重的估计值等,这样作出的图形称为残差图.在残差图中,残差点 地落在水平的带状区域中,说明选用的模型比较合适,这样的带状区域的宽度 ,说明模型拟合精度越高.(2)残差平方和法残差平方和∑ (yi-y i)2,残差平方和 ,模型拟合效果越好.(3)利用 R2刻画回归效果R2= ;R2表示 变量对于 变量变化的贡献率.R2越接近于 ,表示回归的效果越好.课内探究案一、新课导学:1探究点一 线性回归方程问题 1 两个变量之间的关系分几类?问题 2:什么叫回归分析?问题 3: 对具有线性相关关系的两个变量进行回归分析有哪几个步骤?探究点二 线性回归分析问题 1 利用求得的回归方程进行预报,为什么得到的预报值和实际值并不相同?问题 2: 给出两个变量的回归方程,怎样判断拟合效果的 好坏?问题 3: 如果 R2≈0.64,表示什么意义?二、合作探究例 1 : 若从某大学中随机选取 8 名女大学生,其身高和体重数据如下表所示:编号12345678身高/cm165165157170175165155170体重/kg4857505464614359求根据女大学生的身高预报体重的回归方程,并预报一名身高为 172 cm 的女大学生的体重.2例 2 : 某运动员训练次数与运动成绩之间的数据关系如 下:次数(x)303335373 9444650成绩(y)3 034373942464851(1)作...