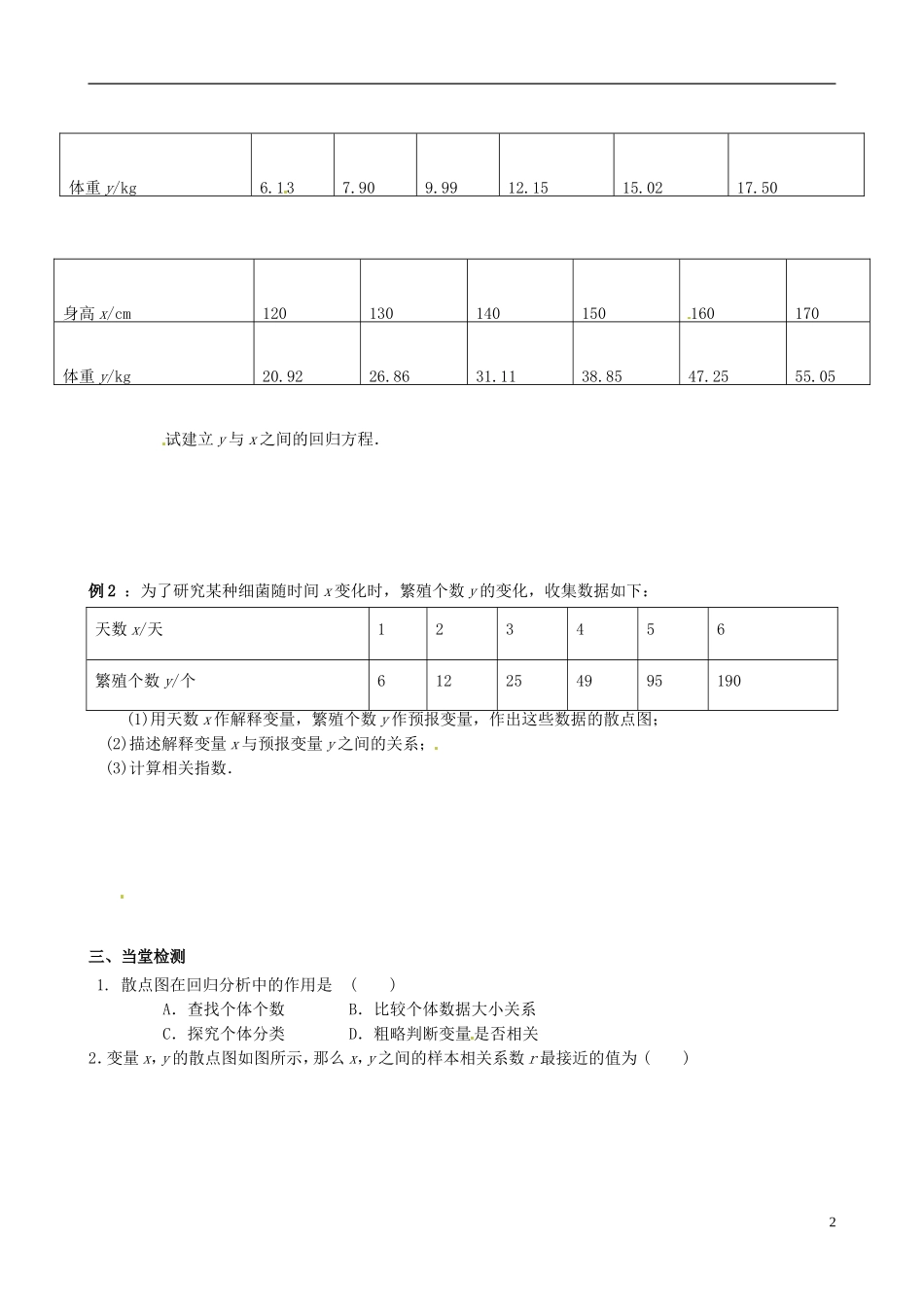
§3.1.2 回归分析的基本思想及其初步运用学习目标 :1.进一步体会回归分析的基本思想.2.通过非线性回归分析,判断几种不同模型的拟合程度.学习重点:体会回归分析的基本思想.学习难点:通过非线性回归分析,判断几种不同模型的拟合程度.课前预习案教材助读:阅读教材的内容,思考并完成下列问题:1.如果两个变量不呈现线性相关关系,常见的两个变量间的关系还有指数关系、二次函数关系.2.两个变量间的非线性关系可以通过对解释变量的变换(对数变换、平方变换等)转化为另外两个变量的 关系.3.比较不同模型的拟合效果,可以通过 的大小, 的大小.课内探究案一、新课导学:探究点一 非线性回归模型问题 1:有些变量间的关系并不是线性相关,怎样确定回归模型?问题 2:如果两个变量呈现非线性相关关系,怎样求出回归 方程?探究点二 非线性回归分析问题 1:对于两个变量间的相关关系,是否只有唯一一种回归模型来拟合它们间的相关关系?问题 2:对同一个问题建立的两种不同回归模型,怎样比较它们的拟合效果?二、合作探究例 1 : 某地区不同身高的未成年男性的体重平均值如下表:身高 x/cm607080901001101体重 y/kg6.137.909.9912.1515.0217.50身高 x/cm120130140150160170体重 y/kg20.9226.8631.1138.8547.2555.05试建立 y 与 x 之间的回归方程.例 2 :为了研究某种细菌随时间 x 变化时,繁殖个数 y 的变化,收集数据如下:天数 x/天123456繁殖个数 y/个612254995190(1)用天数 x 作解释变量,繁殖个数 y 作预报变量,作出这些数据的散点图;(2)描述解释变量 x 与预报变量 y 之间的关系;(3)计算相关指数.三、当堂检测1. 散点图在回归分析中的作用是( )A.查找个体个数 B.比较个体数据大小关系C.探究个体分类 D.粗略判断变量是否相关2.变量 x,y 的散点图如图所示,那么 x,y 之间的样本相关系数 r 最接近的值为 ( )2A.1 B.-0.5 C.0 D.0.5四、课后反思课后训练案1. 变量 x 与 y 之间的回归方程表示( )A.x 与 y 之间的函数关系 B.x 与 y 之间的不确定性关系C.x 与 y 之间的真实关系形式 D.x 与 y 之间的真实关系达到最大限度的吻合2. 非线性回归分析的解题思路是______________________.3