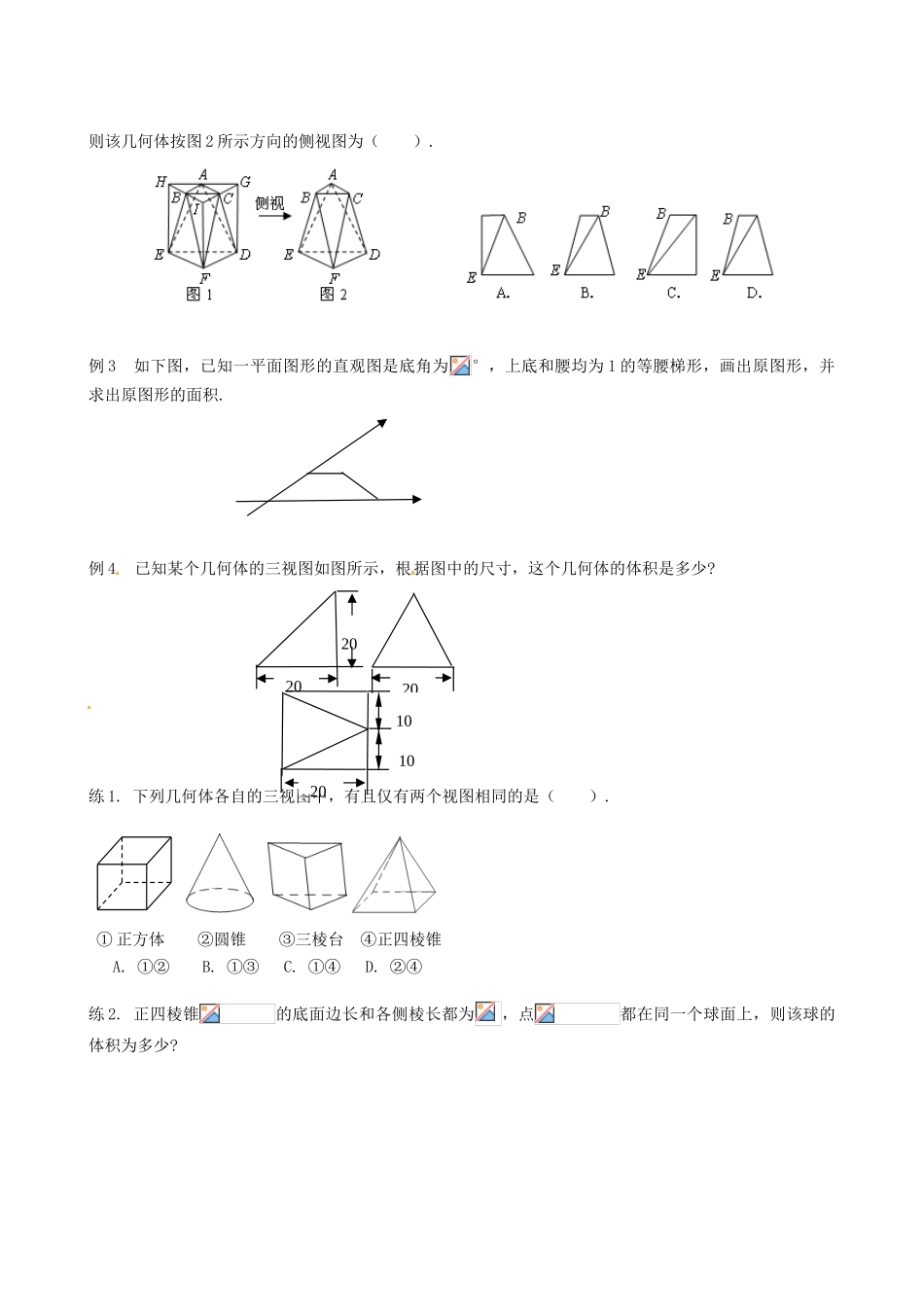
第一章 空间几何体(复习)学习目标:1. 认识柱、锥、台、球及其简单组合体的结构特征,能运用这些特征描述现实生活中简单物体的结构;2. 能画出简单空间图形的三视图,能识别三视图所表示的立体模型;3. 会用斜二侧画法画几何体的直观图;4. 会求简单几何体的表面积和体积.学习重点:各空间几何体的特征,计算公式,空间图形的画法。学习难点:空间想象能力的建立,空间图形的识别与应用。课前预习(预习教材 P2~ P37,找出疑惑之处)复习 1:空间几何体的结构① 多面体、旋转体有关概念;② 棱柱、棱锥、棱台结构特征及其分类;③ 圆柱、圆锥、圆台结构特征;④ 球的结构特征;⑤ 简单组合体的结构特征.复习 2:空间几何体的三视图和直观图① 中心投影与平行投影区别,正投影概念;② 三视图的画法:长对正、高平齐、宽相等;③ 斜二测画法画直观图:轴与轴夹角,平行于轴长度不变,平行于轴长度减半;复习 3:空间几何体的表面积与体积① 柱体、锥体、台体表面积求法(利用展开图);② 柱体、锥体、台体的体积公式;③ 球的表面积与体积公式.课内探究 例 1 在正方体上任意选择 4 个顶点,它们可能是如下各种几何体的 4 个顶点,这些几何体是______.(写出所有正确结论的编号)① 矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四边体;④每个面都是等边三角形的四边体;⑤每个面都是直角三角形的四面体.例 2 将正三棱柱截去三个角(如图 1 所示,、、分别是三边的中点)得到几何体如图 2,则该几何体按图 2 所示方向的侧视图为( ).例 3 如下图,已知一平面图形的直观图是底角为°,上底和腰均为 1 的等腰梯形,画出原图形,并求出原图形的面积.例 4 已知某个几何体的三视图如图所示,根据图中的尺寸,这个几何体的体积是多少?练 1. 下列几何体各自的三视图中,有且仅有两个视图相同的是( ). ① 正方体 ②圆锥 ③三棱台 ④正四棱锥 A. ①② B. ①③ C. ①④ D. ②④练 2. 正四棱锥的底面边长和各侧棱长都为,点都在同一个球面上,则该球的体积为多少?202020102010练 3. 一个用鲜花做成的花柱,它的下面是一个直径为、高为的圆柱形物体,上面是一个半球形体,如果每平方米大约需要鲜花朵,那么装饰这个花柱大约需要多少朵鲜花(取)?当堂检测1. 已知是一个直角三角形,则经过平行投影后所得三角形是( ).A.直角三角形 B.锐角三角形...