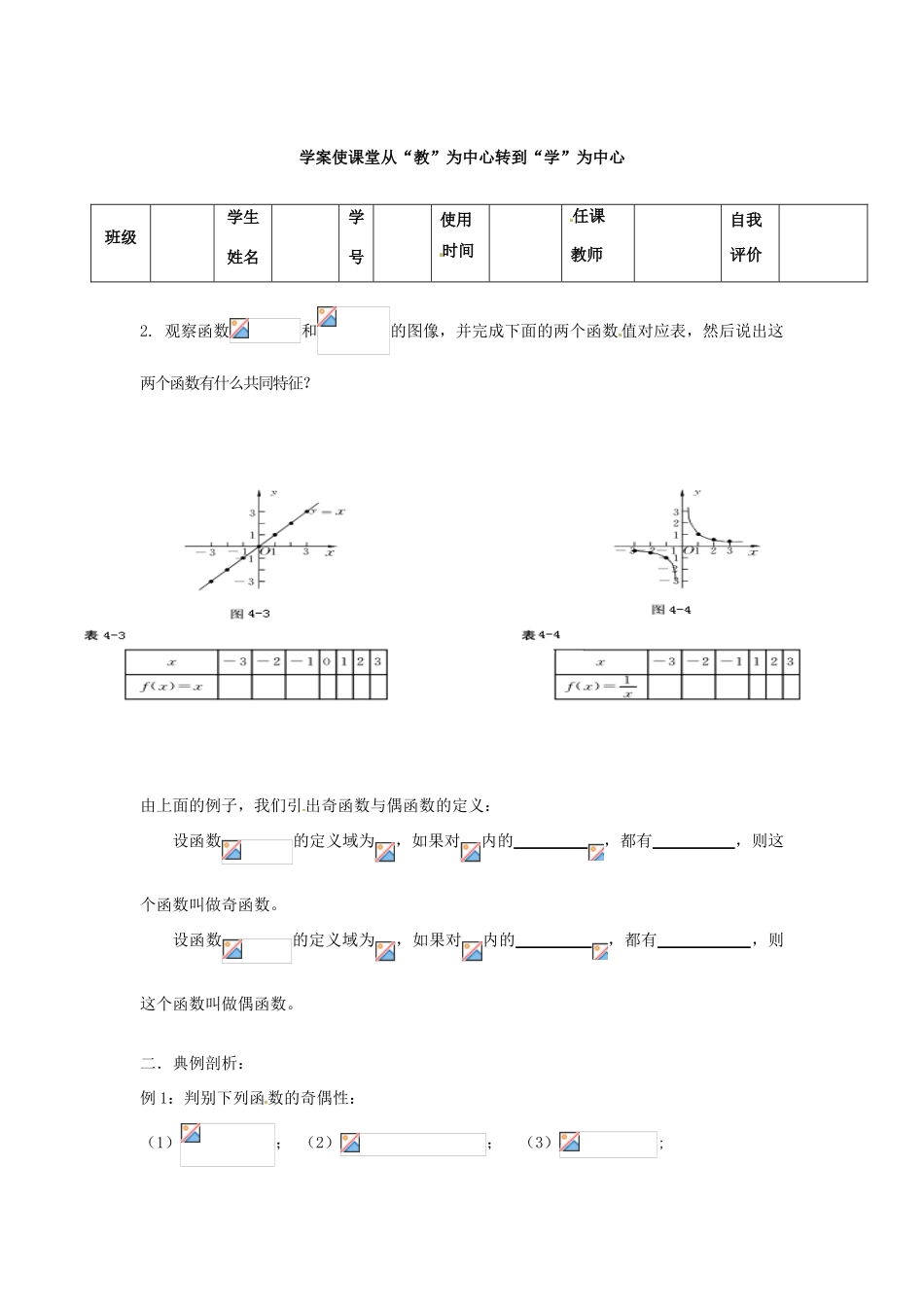
山东省临朐县实验中学高中数学 函数的奇偶性学案 新人教 A 版必修 1学习目标:1.结合具体函数,了解奇偶性的含义;2.学会运用函数 图像理解和研究函数的性质,理解奇函数、偶函数的几何意义,能熟练判别函数的奇偶性。重点难点:学习重点:函数奇偶性的概念。学习难点:函数奇偶性的判断。知识链接:1.轴对称图形:2.中心对称图形:学习过程:一.课内探究:1.观察如下两图,思考并讨论以下问题:(1)这两个函数图像有什么共同特征?(2)相应的两个函数值对应表是如何体现这些特征的?学案使课堂从“教”为中心转到“学”为中心班级学生姓名学号使用时间任课教师自我评价2. 观察函数和的图像,并完成下面的两个函数 值对应表,然后说出这两个函数有什么共同特征?由上面的例子,我们引出奇函数与偶函数的定义:设函数的定义域为,如果对内的 ,都有 ,则这个函数叫做奇函数。设函数的定义域为,如果对内的 ,都有 ,则这个函数叫做偶函数。二.典例剖析:例 1:判别下列函数的奇偶性:(1); (2); (3);( 4) ; (5); (6)导读、 导听、 导思、 导做例 2:已知是奇函数,是偶函数,且,求,.例 3::已知是偶函数,时,,求时的解析式例 4:已知函数是偶函数,且在上 是减函数,判断在上是增函数,还是减函数,并证明你的结论.学案使学生从“听众”角色转变为“演员”角色例 5:设函数是定义在上的奇函数,且在区间上是减函数,实数满足不等式,求实数的取值范围.三.小结反思:四.当堂检测:1. 函数的图象关于 对称2. 已知函数是偶函数且定义域为则 3. 已知是奇函数,且当时,求在上的表达式4. 已知在R上是偶函数,在区间上递增且求的取值范围五.课后巩固:P49: 练习 A. B 六.学习后记:自学、 自问、 自做、 自练