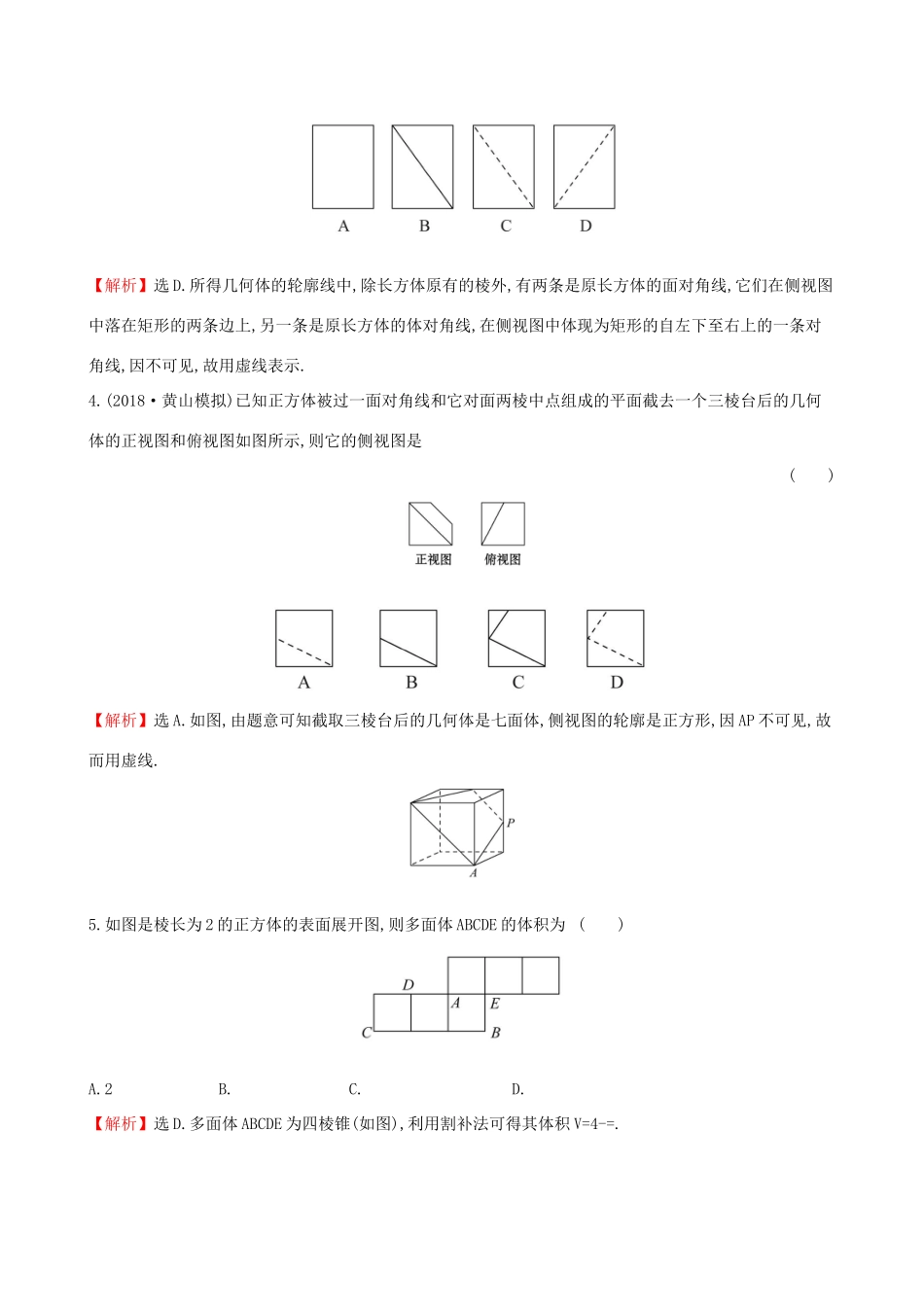
第七章立体几何初步单元过关检测(七)(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设a,b是平面α内两条不同的直线,l是平面α外的一条直线,则“l⊥a,l⊥b”是“l⊥α”的()A.充要条件B.充分而不必要条件C.必要而不充分条件D.既不充分也不必要条件【解析】选C.若a,b是平面α内两条不同的直线,l是平面α外的一条直线,l⊥a,l⊥b,a∥b,则l可以与平面α斜交,推不出l⊥α.若l⊥α,a,b是平面α内两条不同的直线,l是平面α外的一条直线,则l⊥a,l⊥b.所以“l⊥a,l⊥b”是“l⊥α”的必要不充分条件.2.关于空间两条直线a,b和平面α,下列命题正确的是()A.若a∥b,b⊂α,则a∥αB.若a∥α,b⊂α,则a∥bC.若a∥α,b∥α,则a∥bD.若a⊥α,b⊥α,则a∥b【解析】选D.线面平行的判定定理中的条件要求a⊄α,故A错;对于线面平行,这条直线与面内的直线的位置关系可以平行,也可以异面,故B错;平行于同一个平面的两条直线的位置关系:平行、相交、异面都有可能,故C错;垂直于同一个平面的两条直线是平行的,故D正确.3.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为()【解析】选D.所得几何体的轮廓线中,除长方体原有的棱外,有两条是原长方体的面对角线,它们在侧视图中落在矩形的两条边上,另一条是原长方体的体对角线,在侧视图中体现为矩形的自左下至右上的一条对角线,因不可见,故用虚线表示.4.(2018·黄山模拟)已知正方体被过一面对角线和它对面两棱中点组成的平面截去一个三棱台后的几何体的正视图和俯视图如图所示,则它的侧视图是()【解析】选A.如图,由题意可知截取三棱台后的几何体是七面体,侧视图的轮廓是正方形,因AP不可见,故而用虚线.5.如图是棱长为2的正方体的表面展开图,则多面体ABCDE的体积为()A.2B.C.D.【解析】选D.多面体ABCDE为四棱锥(如图),利用割补法可得其体积V=4-=.6.封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是()A.4πB.C.6πD.【解析】选B.由题意知,底面三角形的内切圆直径为4,三棱柱的高为3,所以球的最大直径为3,V的最大值为.7.一个几何体的三视图及其尺寸如图所示,则该几何体的表面积为()A.16B.8+8C.2+2+8D.4+4+8【解析】选D.由三视图知,该几何体是底面边长为=2的正方形,高PD=2的四棱锥P-ABCD,因为PD⊥平面ABCD,且四边形ABCD是正方形,易得BC⊥PC,BA⊥PA,又PC===2,所以S△PCD=S△PAD=×2×2=2,S△PAB=S△PBC=×2×2=2.所以几何体的表面积为4+4+8.8.在梯形ABCD中,∠ABC=,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为()A.B.C.D.2π【解析】选C.过点C作CE垂直于AD所在直线于点E,梯形ABCD绕AD所在直线旋转一周而形成的旋转体是由以线段AB的长为底面圆半径,线段BC为母线的圆柱挖去以线段CE的长为底面圆半径,ED为高的圆锥而成,如图所示,该几何体的体积为V=V圆柱-V圆锥=π·AB2·BC-π·CE2·DE=π×12×2-π×12×1=.9.在正三棱锥S-ABC中,点M是SC的中点,且AM⊥SB,底面边长AB=2,则正三棱锥S-ABC的外接球的表面积为()A.6πB.12πC.32πD.36π【解析】选B.因为三棱锥S-ABC为正三棱锥,所以SB⊥AC,又AM⊥SB,AC∩AM=A,所以SB⊥平面SAC,所以SB⊥SA,SB⊥SC,同理,SA⊥SC,即SA,SB,SC三线两两垂直,且AB=2,所以SA=SB=SC=2,所以(2R)2=3×22=12,所以球的表面积S=4πR2=12π.10.如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD,将其沿对角线BD折成四面体A′BCD,使平面A′BD⊥平面BCD,若四面体A′BCD的顶点在同一个球面上,则该球的体积为()A.πB.3πC.πD.2π【解析】选A.如图所示,取BD的中点E,BC的中点O,连接A′E,EO,A′O,OD.因为平面A′BD⊥平面BCD,A′E⊥BD,平面A′BD∩平面BCD=BD,A′E⊂平面A′BD,所以A′E⊥平面BCD.因为A′B=A′D=CD=1,BD=,所以A′E=,EO=,所以OA′=.在Rt△BCD中,OB=OC=OD=BC=,所以四面体A′BCD的外接球的球心为O,球的半径为,所以V球=π×=π.11.如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD.则在三棱锥A-BCD中,下列命题正确的是()A.平面ABD...