山东省巨野县第一中学高中数学 3.1.5 空间向量运算的坐标表示学案 新人教A版必修2VIP专享

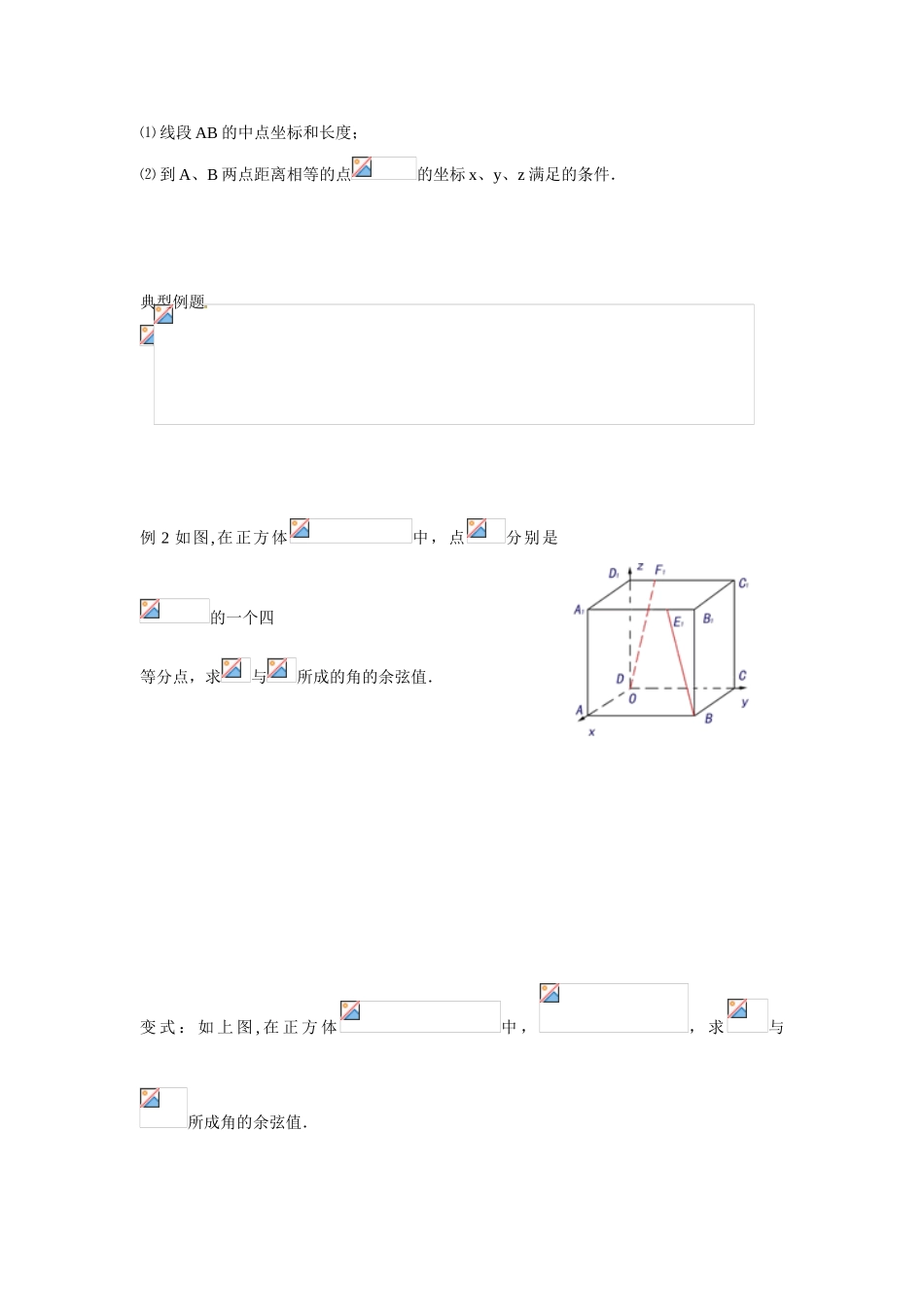
山东省巨野县第一中学高中数学 3.1.5 空间向量运算的坐标表示学案 新人教 A 版必修 2 学习目标 1 理解空间向量坐标的概念，会确定一些简单几何体的顶点坐标．2 掌握空间向量的坐标运算规律，会判断两个向量的共线或垂直．3 掌握空间向量的模、夹角公式和两点间距离公式，并能运用这些知识解决一些相关问题．重点 空间向 量的坐标运算．难点 利用空间向量的坐标运算解决直线、平面间的位置关系，夹角、模的问题．一．课前预习（预学案）1．空间向量的加减和数乘的坐标表示．设 a＝(a1，a2，a3)，b＝(b1，b2，b3)．(1)a＋b＝______________________；(2)a－b＝______________________；(3)λa＝__________________(λ∈R)；(4)若 b≠0，则 a∥b ⇔ a＝λb(λ∈R)⇔____________，____________，____________2．空间向量数量积的坐标表示及夹角公式．若 a＝(a1，a2，a3)，b＝(b1，b2，b3)，则：(1)a·b＝____________________；(2)|a|＝＝________________；(3)cos〈a，b〉＝＝__________________________；(4)a⊥b⇔____________________.3．空间中向量的坐标及两点间的距离公式．在空间直角坐标系中，设 A(a1，b1，c1)，B(a2，b2，c2)．(1)AB＝____________________；(2)dAB＝|AB|＝________________________.二、新课导学 学习探究（导学案）探究任务一：空间向量坐标表示夹角和距离公式问题：在空间直角坐标系中，如何用坐标求线段的长度和两个向量之间的夹角？新知：1. 向量的模：设 a＝，则｜a｜＝ 2. 两个向量的夹角公式：设 a＝， b＝，由向 量数量积定义： a·b＝|a||b|cos＜a,b＞，又由向量数量积坐标运算公式：a·b＝ ，由此可以得出：cos＜a,b＞＝ 试试：① 当 cos＜a、b＞＝1 时，a 与 b 所成角是 ；② 当 cos＜a、b＞＝－1 时，a 与 b 所成角是 ；③ 当 cos＜a、b＞＝0 时，a 与 b 所成角是 ，即 a 与 b 的位置关系是 ，用符号表示为 .反思：设 a＝，b＝，则⑴ a//B. a 与 b 所成角是 a 与 b 的坐标关系为 ；⑵ a⊥ba 与 b 的坐标关系为 ；3. 两点间的距离公式：在空间直角坐标系中，已知点，，则线段 AB 的长度为：AB= 4. 线段中点的坐标公式：在空间直角坐标系中，已知点，，则线段 AB 的中点坐标为: .探究任务二练习 1. 已知 A(3,3,1)、B(1，0，5)，求：⑴ 线段 AB 的中点坐标和长度；⑵ 到 A、B 两点距离相等的点的坐标 x、y、z 满...