山东省淄博市淄川般阳中学高中数学 3.3.1函数的单调性与导数2学案 新人教A版选修1-1

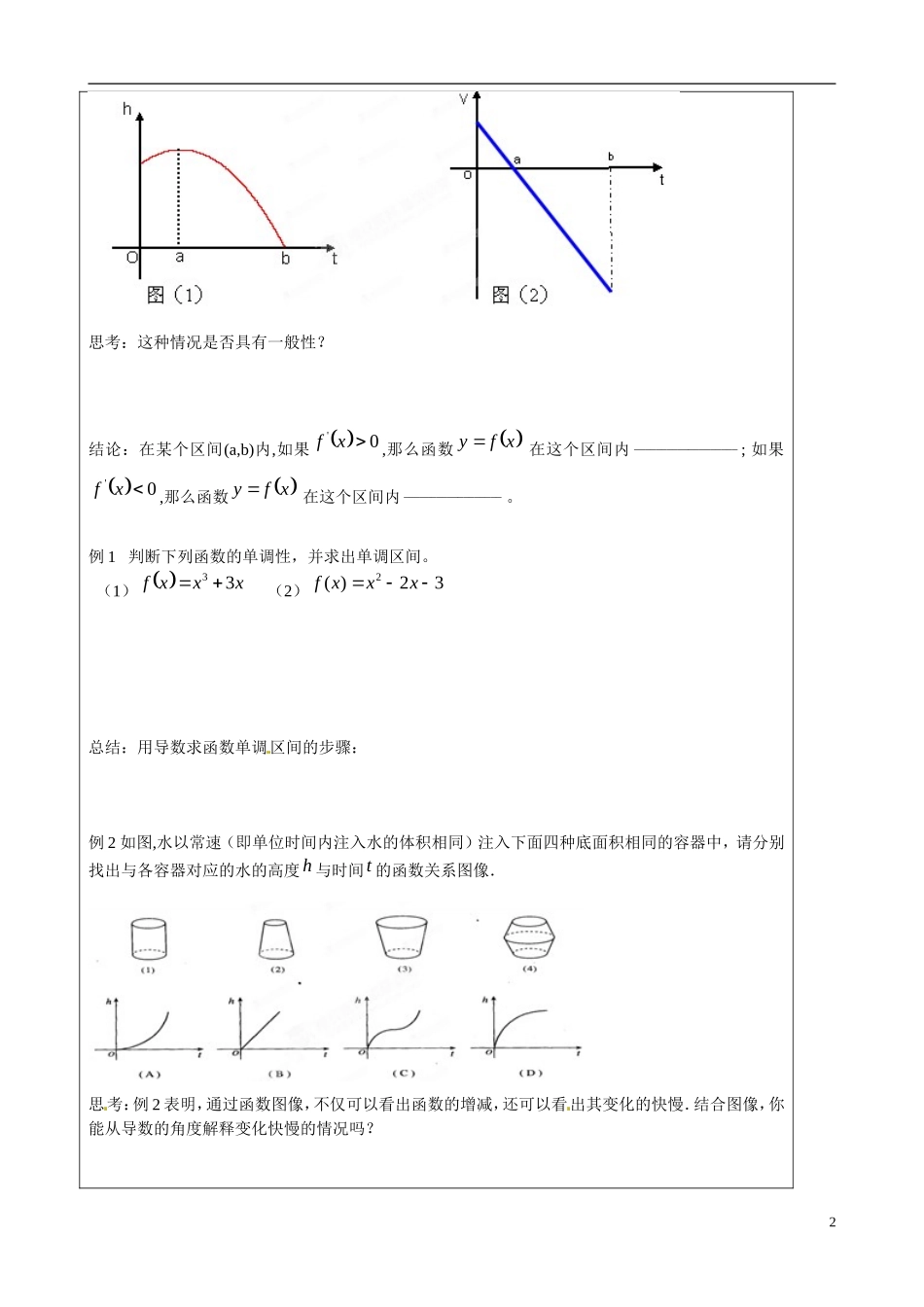
山东省淄博市淄川般阳中学高中数学 3.3.1 函数的单调性与导数 2 学案 新人教 A 版选修 1-1 学习目标：1.结合实例，借助几何直观探索函数的单调性与导数的关系； 2.掌握利用导数判断函数单调性的方法。重点难点：利用导数求函数的单调区间和判断函数的单调性。教学模式：“三五五”教学模式教学资源：多媒体、课本Ⅰ、课前：预案：基本初等函数的导数公式'C ；  'nx ； 'sin x ； ；  'xa ；  'xe ； 'logxa ； 'ln x .2．利用导数的符号来判断函数单调性: 一般地，设函数( )yf x在某个区间可导， 如果在这个区间内'( )0fx ，则( )yf x为这个区间内的 ； 如果在这个区间内'( )0fx ，则( )yf x为这个区间内的 。利用导数解释函数增减快慢 一般地，如果一个函数在某一范围内导 数的绝对值较大，那么函数在这个范围内___________________________， 这 时 ， 函 数 的 图 像 比 较_________________； 反 之 ， 函 数 的 图 像 比 较____________________。 Ⅱ、课中：【学情调查 情境导入】函数 xfy 在给定区间ba,上，当baxx,,21且21xx 时 （1）都有   21xfxf，则  xf在ba,上是________________； （2）都有   21xfxf，则  xf在ba,上是________________。2、是否有其他判断函数单调性的方法？【问题展示 合作探究】探究一：函数的导数与函数单调性的关系下图（1）是高台跳水运动员的高度 h 随时间 t 变化的函数  105.69.42ttth的图像，图（2）是速度 v 随时间变化的函数是   5.68.9'tthtv的图像。 运动员从起跳到最高点, 以及从最高点到入水这两段时间的运动状态有什么区别?1思考：这种情况是否具有一般性？结论：在某个区间(a,b)内,如果 0'xf,那么函数 xfy  在这个区间内___________________; 如果 0'xf,那么函数 xfy  在这个区间内__________________。例 1 判断下列函数的单调性，并求出单调区间。 （1）  xxxf33  （2）32)(2xxxf总结：用导数求函数单调区间的步骤： 例 2 如图,水以常速（即单位时间内注入水的体积相同）注入下面四种底面积相同的容器中，请分别找出与各容器对应的水的高度h 与时间t 的函数关系图像．思考：例 2 表明，通...