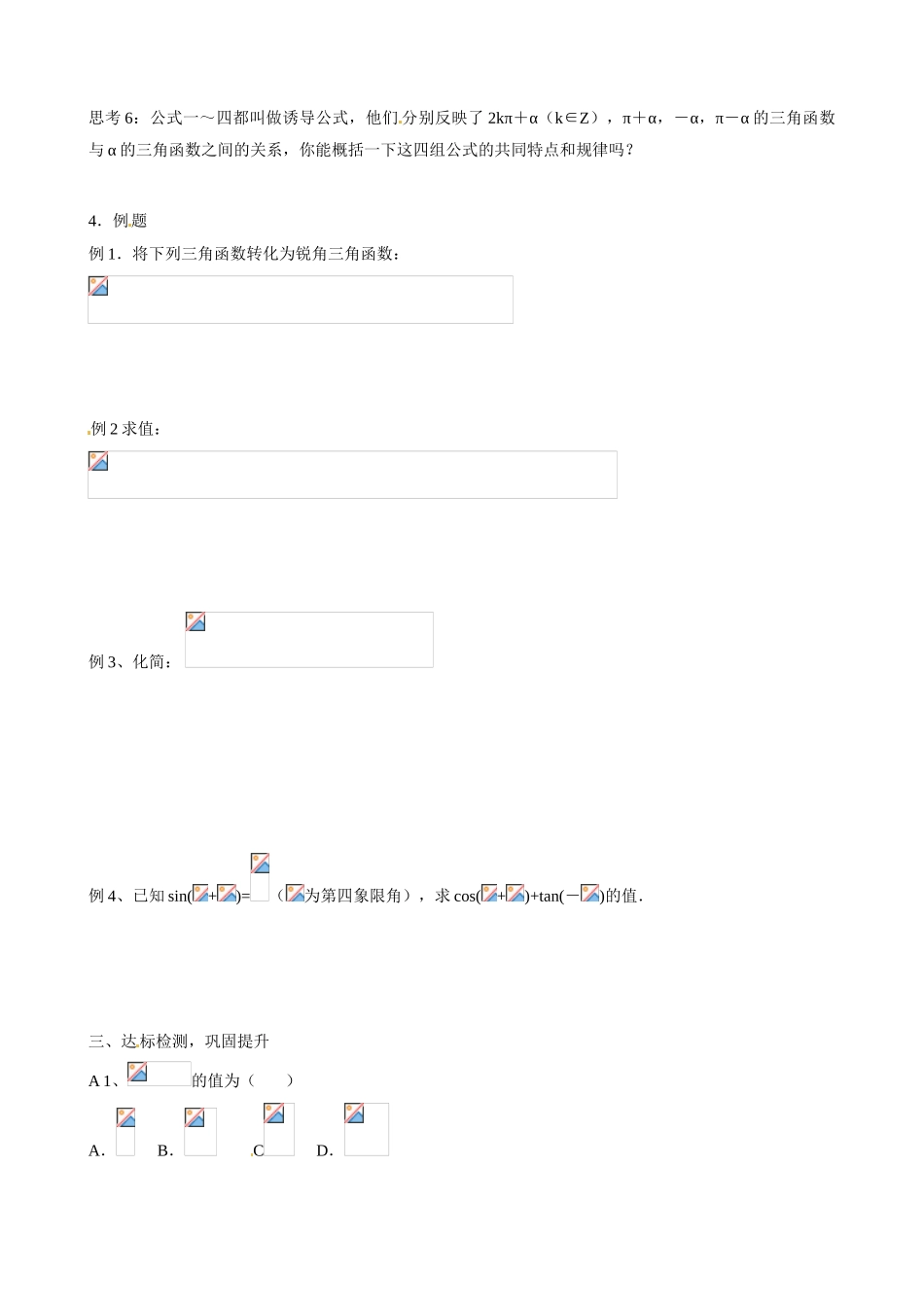
山东省淄博市淄川般阳中学高中数学 第 1 章《三角函数》1.3.1 三角函数的诱导公式 1 学案新人教 A 版必修 4一、预习目标:1. 诱导公式的探究,理解和掌握公式的内涵及结构特征,;2.会初步运用诱导公式进行简单三角函数式的求值、化简与恒等式的证明二、预习内容:阅读教材填空:1.公式二 , , .2.公式三 , , .3.公式四 , , .我们可以用一段话来概括公式一~四:+(),,的三角函数值,等于 ,前面加上一个 .(二) 学案学习重点:诱导公式的推导及应用.学习难点:相关角边的几何对称关系及诱导公式结构特征的认识.一、学情调查,情景导入1.试写出诱导公式(一)并说出它的结构特征2. 角 α 的终边与单位圆交于点 P(x, y),则:sinα= ;cosα= ;tanα= 。3. 试求下列三角函数的值(1)sin1110° (2)sin1290°二、问题展示,合作探究探究一:π+α 的诱导公式 思考下列问题 1:(1)210°能否用(180°+)的形式表达?(2)210°角的终边与 30°的终边关系如何?(3)设 210°、30°角的终边分别交单位圆于点 p、p',则点 p 与 p'的位置关系如何?(4)设点 p(x,y),则点 p'怎样表示? (5)sin210°与 sin30°的值关系如何?思考 7:该公式有什么特点,如何记忆?探究二:-α,π-α 的诱导公式: 思考 1:对于任意给定的一个角 α,-α 的终边与 α 的终边有什么关系? 思考 2:设角 α 的终边与单位圆交于点 P(x,y),则-α 的终边与单位圆的交点坐标如何?思考 3:根据三角函数定义,-α 的三角函数与 α 的三角函数有什么关系?结论 诱导公式(三):思考 4:利用 π-α=π+(-α),结合公式二、三,你能得到什么结论?结论 诱导公式(四):思考 5:公式三、四有什么特点,如何记忆?思考 6:公式一~四都叫做诱导公式,他们 分别反映了 2kπ+α(k∈Z),π+α,-α,π-α 的三角函数与 α 的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗? 4.例题例 1.将下列三角函数转化为锐角三角函数:例 2 求值:例 3、化简: 例 4、已知 sin(+)=(为第四象限角),求 cos(+)+tan(-)的值.三、达标检测,巩固提升A 1、的值为( ) A. B. C D.A2、的值等于( ) A. B. C. D.A3.求值:(1) (2)B4、下列各式不正确的是( )sin(+180°)=-sinα B.cos(-+β)=-cos(-β)C. sin(--360°)=-sinα D.cos(--β)=cos(+β)C5、若则的值是( )A. B. C. D.