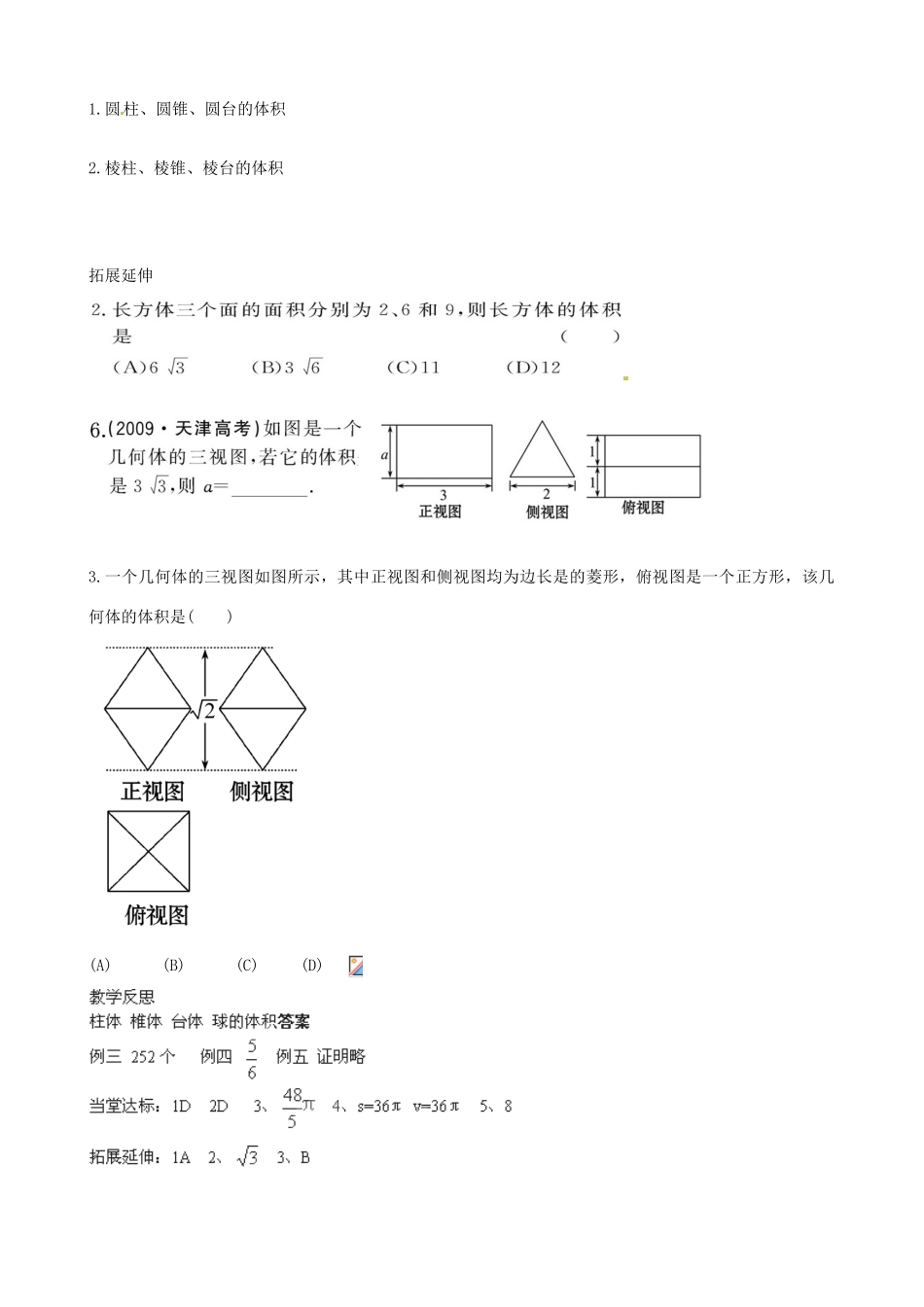
山东省泰安市肥城市第三中学高一数学人教 A 版必修 2 学案:1.3.1 柱体 锥体 台体的体积学案【学习目标】【回顾·预习】1、柱体、锥体、台体、球的结构特征2、以前学习的柱体的体积 【自主·合作·探究】1 正方体、长方体和圆柱的体积公式V=2.圆锥、棱锥的体积公式 V =3、棱台、圆台的体积公式 V=4、球的体积公式 已知球的半径为 R,则球的体积为二、典型例题 【例 4】如下图,在长方体中,截下一个棱锥,求棱锥的体积与剩余部分的体积之比.例 5 圆柱的底面直径与高都等于球的直径求证:(1)球的体积等于圆柱体积的(2)球的表面积等于圆柱的侧面积【当堂达标】 1.长方体的过一个顶点的三条棱长的比是 1∶2∶3,对角线长为 2,则这个长方体的体积是( )(A)6 (B)12 (C)24 (D)48圆 2. 圆台上、下底面面积分别是、4,侧面积是 6,则圆台的体积是( ) A.A. B. C. D. 3.如图,在三角形 ABC 中,若 AC=3,BC=4,AB=5,以 AB 所在直线为轴,将此三角形旋转一周,求所得旋转体的体积.4、.若棱长为的正方体的各个顶点都在同一个球面上, 求该球的体积和表面积 .5、将一个球的半径扩大一倍,它的体积扩大到原来的 倍【反思·提升】1.圆柱、圆锥、圆台的体积2.棱柱、棱锥、棱台的体积拓展延伸 3.一个几何体的三视图如图所示,其中正视图和侧视图均为边长是的菱形,俯视图是一个正方形,该几何体的体积是( )(A) (B) (C) (D)