山东省泰安市肥城市第三中学2013-2014学年高一数学 y=Asin（wx+φ）的图像复习学案

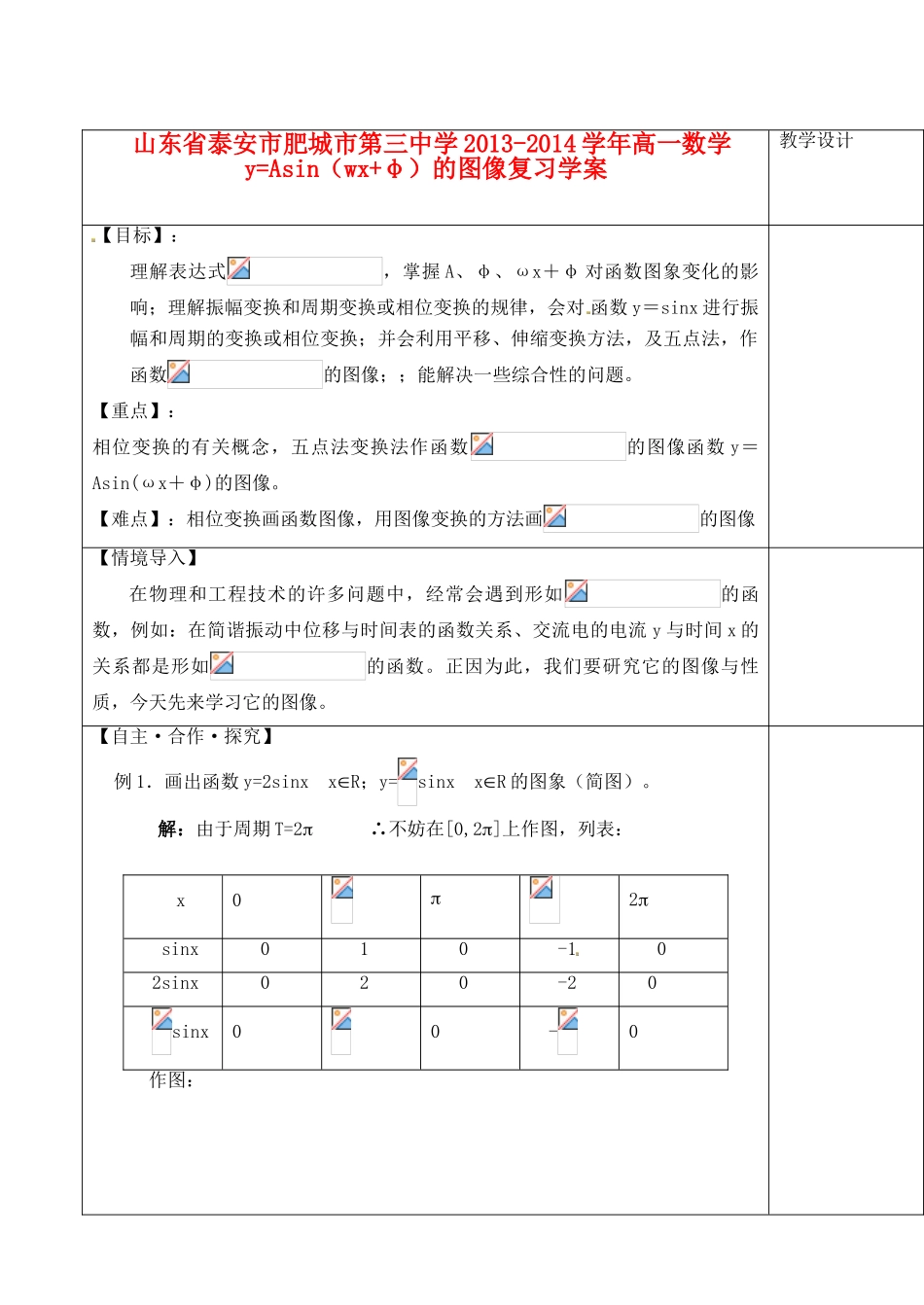
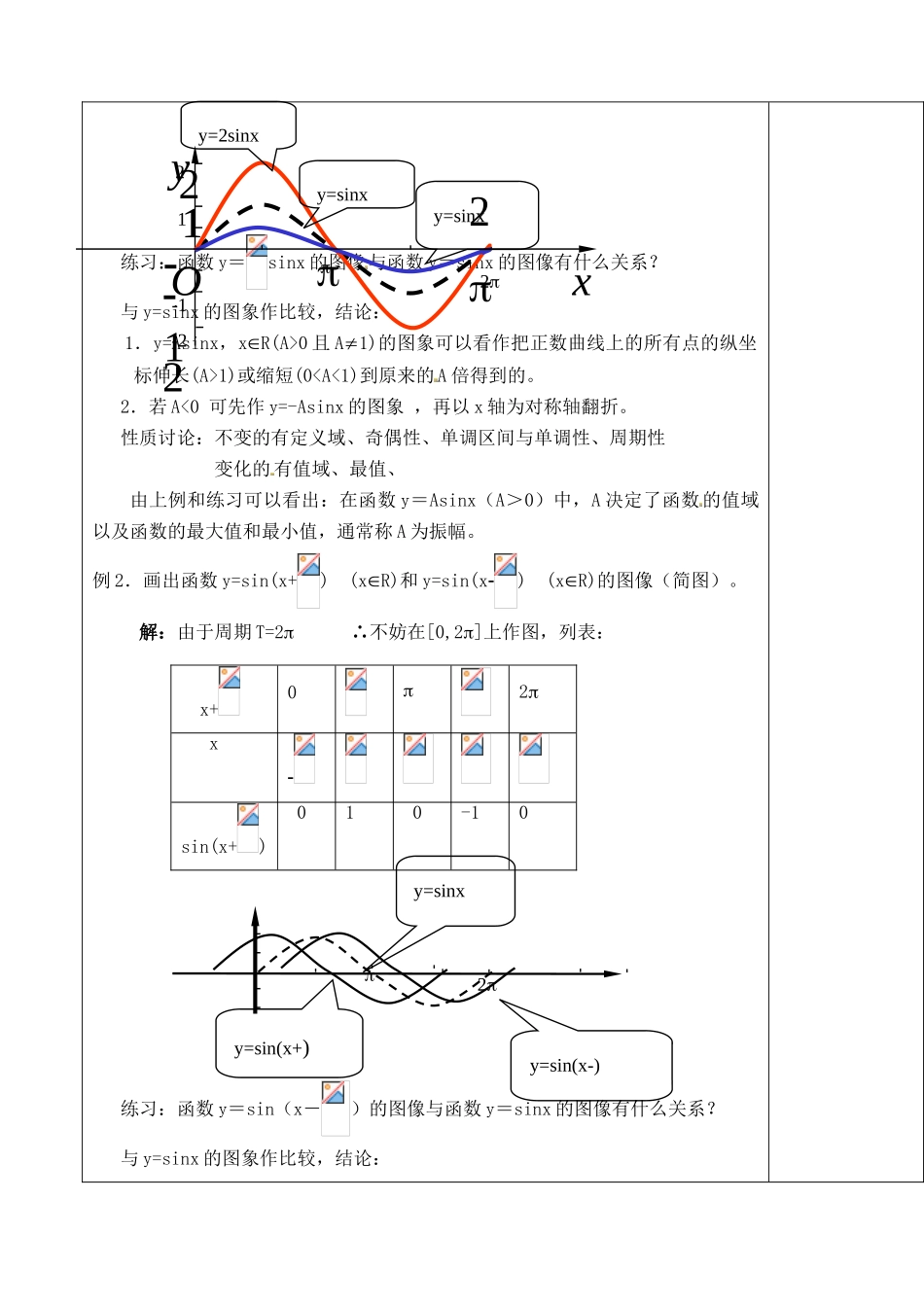
山东省泰安市肥城市第三中学 2013-2014 学年高一数学 y=Asin（wx+φ）的图像复习学案教学设计【目标】： 理解表达式，掌握 A、φ、ωx＋φ 对函数图象变化的影响；理解振幅变换和周期变换或相位变换的规律，会对 函数 y＝sinx 进行振幅和周期的变换或相位变换；并会利用平移、伸缩变换方法，及五点法，作函数的图像；；能解决一些综合性的问题。【重点】：相位变换的有关概念，五点法变换法作函数的图像函数 y＝Asin(ωx＋φ)的图像。【难点】：相位变换画函数图像，用图像变换的方法画的图像【情境导入】在物理和工程技术的许多问题中，经常会遇到形如的函数，例如：在简谐振动中位移与时间表的函数关系、交流电的电流 y 与时间 x 的关系都是形如的函数。正因为此，我们要研究它的图像与性质，今天先来学习它的图像。【自主·合作·探究】例 1．画出函数 y=2sinx xR；y=sinx xR 的图象（简图）。 解：由于周期 T=2 ∴不妨在[0,2]上作图，列表：作图：x02 sinx 0 1 0 -1 0 2sinx 0 2 0 -20 sinx00-0练习：函数 y＝sinx 的图像与函数 y＝sinx 的图像有什么关系？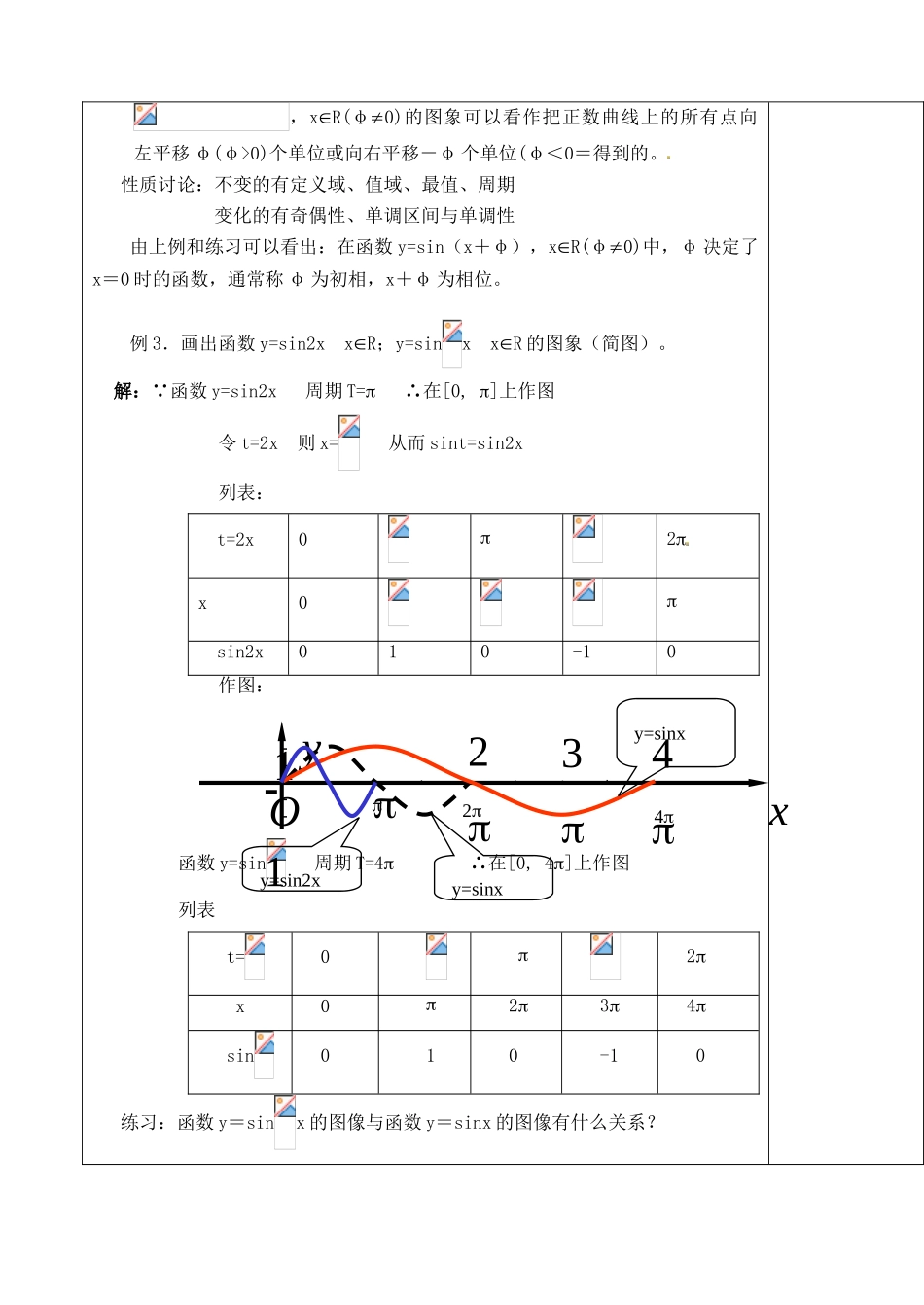与 y=sinx 的图象作比较，结论：1．y=Asinx，xR(A>0 且 A1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A>1)或缩短(00)个单位或向右平移－φ 个单位(φ＜0＝得到的。性质讨论：不变的有定义域、值域、最值、周期 变化的有奇偶性、单调区间与单调性由上例和练习可以看出：在函数 y=sin（x＋φ），xR(φ0)中，φ 决定了x＝0 时的函数，通常称 φ 为初相，x＋φ 为相位。...