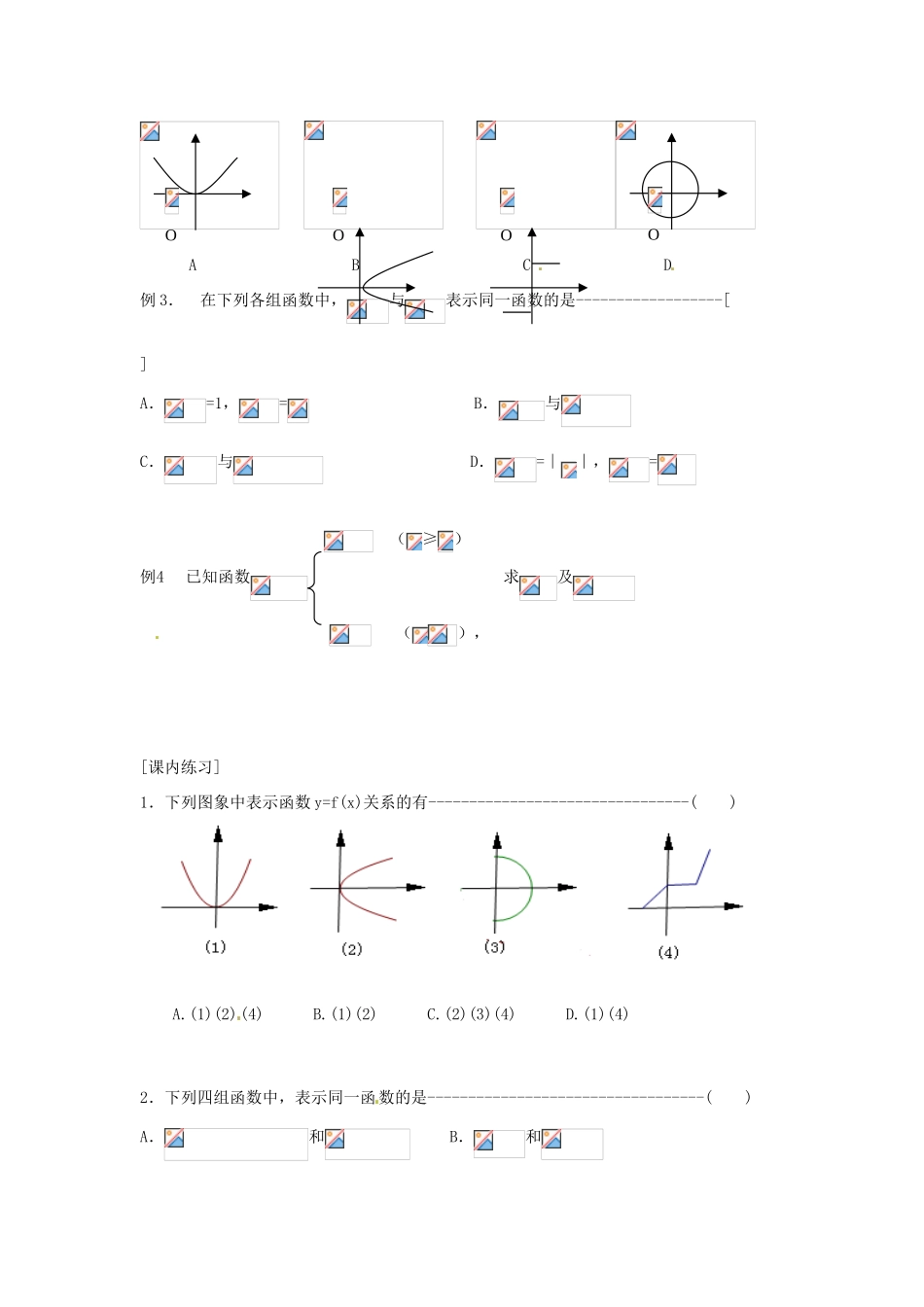
山东省高密市第二中学高中数学《2.1.1 函数的概念与图象(1)》学案 苏教版必修 1[自学目标]1.体会函数是描述变量之间的依赖关系的重要数学模型,理解函数的概念;2.了解构成函数的要素有定义域、值域与对应法则;[知识要点]1.函数的定义:,.2.函数概念的三要素:定义域、值域与对应法则.3.函数的相等.[预习自测]例 1.判断下列对应是否为函数:(1)(2)这里补充:(1)︱,;(2);(3)︱,;(4)≤≤≤≤分析:判断是否为函数应从定义入手,其关键是是否为单值对应,单值对应的关键是元素对应的存在性和唯一性。例 2. 下列各图中表示函数的是------------------------------------------[] A B C D例 3. 在下列各组函数中,与表示同一函数的是------------------[ ]A.=1,= B.与C.与 D.=∣∣,= (≥)例4 已知函数 求及 (),[课内练习]1.下列图象中表示函数 y=f(x)关系的有--------------------------------( ) A.(1)(2)(4) B.(1)(2) C.(2)(3)(4) D.(1)(4)2.下列四组函数中,表示同一函数的是----------------------------------( )A.和 B.和OOOOC.和 D.和3.下列四个命题(1)f(x)=有意义;(2)表示的是含有的代数式 (3)函数 y=2x(x)的图象是一直线;(4)函数 y=的图象是抛物线,其中正确的命题个数是( )A.1 B.2 C.3 D.04.已知 f(x)=,则 f()= ;5.已知 f 满足 f(ab)=f(a)+ f(b),且 f(2)=,那么= [归纳反思]1.本课时的重点内容是函数的定 义与函数记号的意义,难点是函数概念的理解和正确应用;2.判断两个函 数是否是同一函数,是函数概念的一个重要应用,要能紧扣函数定 义的三要素进行分析,从而正确地作出判断.[巩固提高]1.下列各图中,可表示函数的图象的只可能是--------------------[ ]A B C D2.下列各项中表示同一函数的是-----------------------------------------[ ]A.与 B.=,=C.与D. 21 与3.若(为常数),=3,则=------------------------[ ]A.B.1C.2D.4.设,则等于--------------------------------[ ]A.B.C.D. 5.已知=,则= , = 6.已知=,且,则的定义域是 ,值域是 7.已知= ,则 8.设,求的值9.已知函数求使的的取值范围10.若,,求,§2.1.1 函数的概念与图象(1)预习自测:课内练习: 巩固提高:1.D2.D3.B4.A5. =5; ;6.;7.8. =99.10.;