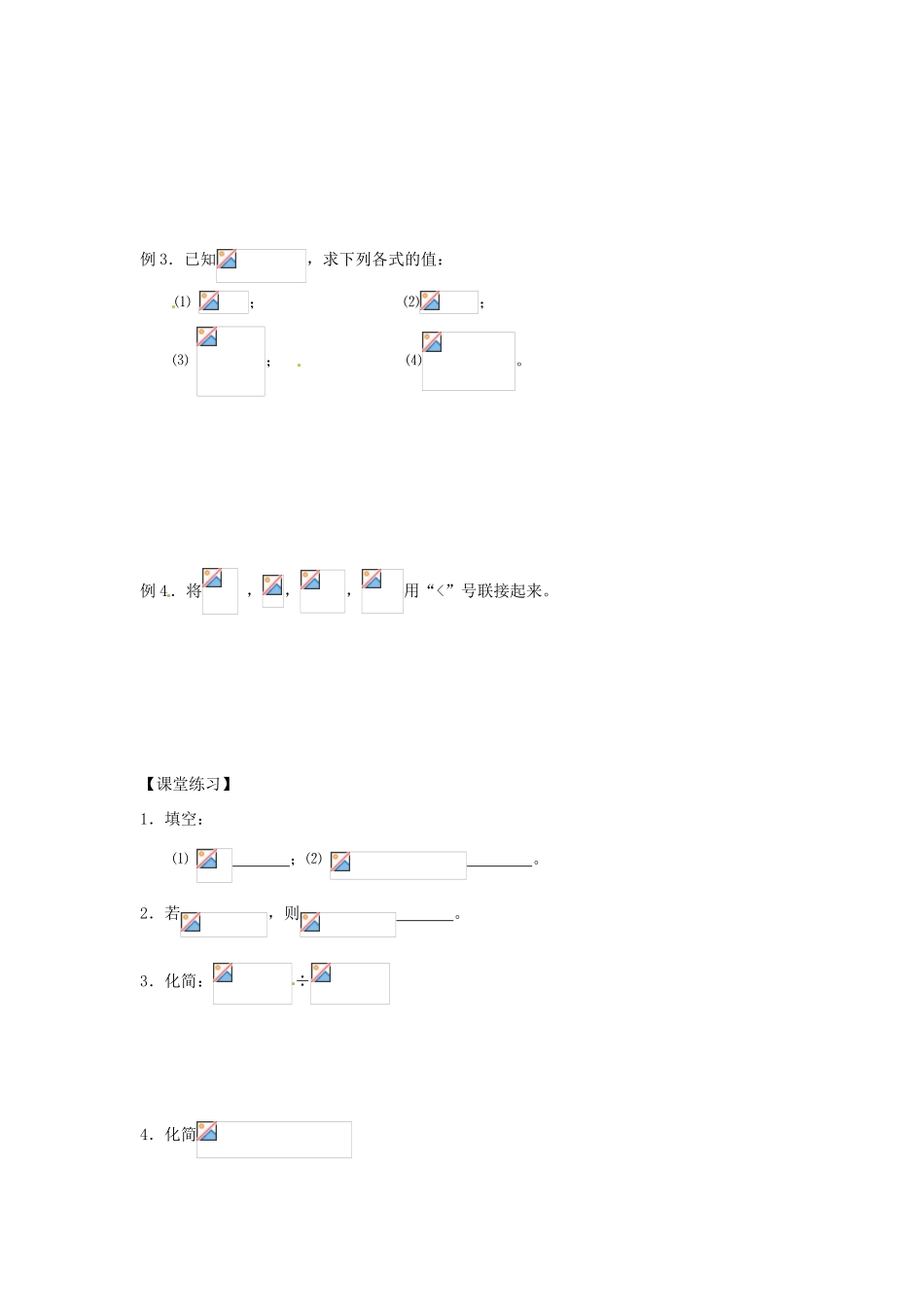
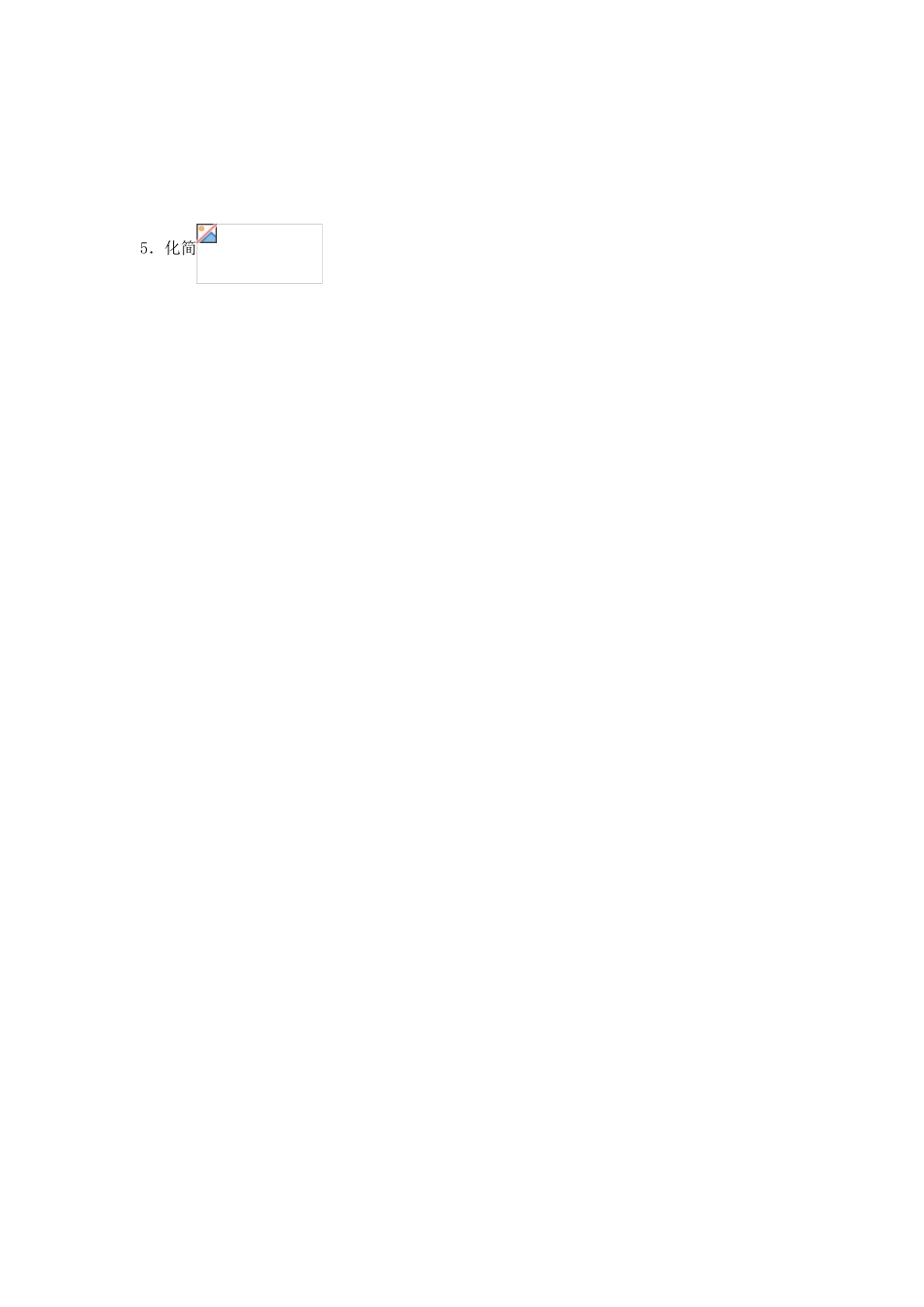
山东省高密市第二中学高中数学《2.2.1 分数指数幂(2)》学案 苏教版必修 1【自学目标】1.理解分数指数幂的意义,熟练掌握根式与分数指数幂的互化方法;2.掌握有理数指数幂的运算性质,灵活地运用运算公式进行有理数指数幂的运算和化简,会进行根式与有理数指数幂的相互转化。【知识描述】1.分数指数幂规定:(1)(,m,m 均为正整数);(2)(,m,m 均为正整数);(3)0 的正分数指数幂为 0,0 的负分数指数幂没有意义。2.有理数指数幂的运算性质设,,,则有:⑴;⑵;⑶。【预习自测】例 1.求下列各式的值:⑴ ; ⑵ ; ⑶ ; ⑷ 例 2.化简下列各式:⑴; ⑵。例 3.已知,求下列各式的值:⑴ ; ⑵;⑶ ; ⑷。 例 4.将 ,,,用“<”号联接起来。【课堂练习】1.填空:⑴ ;⑵ 。2.若,则 。3.化简:÷4.化简5.化简【归纳反思】1.分数指数幂是根式的另一种 表示,根式的运算可利用分数指数幂与根式之间的关系转化为分数指数幂的运算来进行,解题时一般要遵循先化简再计算的原则;2.在进行指数幂运算时,采取 的方法是:化负指数为正指数,化根式为分数 指数幂,化小数为分数进行运算,便于进行乘除、乘方、开方运算可以达到化繁为简的目的。【巩固提高】1.若 a=(2+),b=(2),则(a+1)+(b+1)的值是 ( )A.1 B. C. D.2.下列结论中,正确的命题的是( ) A. = (0) B.a=-C.=(<0) D.()= (a,b)3.化简的结果是( )A. B.ab C. D.a2b4.如果 a,b 都是实数,则下列实数一定成立的是( ) A. B. C. D.5.若,则 。6.将 ,,,用“<”号联接起来是 。 7.计算的值 8.解方程9.化简10.化简÷×2.2.1 分数指数幂(2) 课堂练习: 1. 4; 2. 183. 4. 1 5. 巩固提高: 1-4 DDCB 5. -1 或 26. <<< 7. 1 8. x=-1 9. 24 10. a