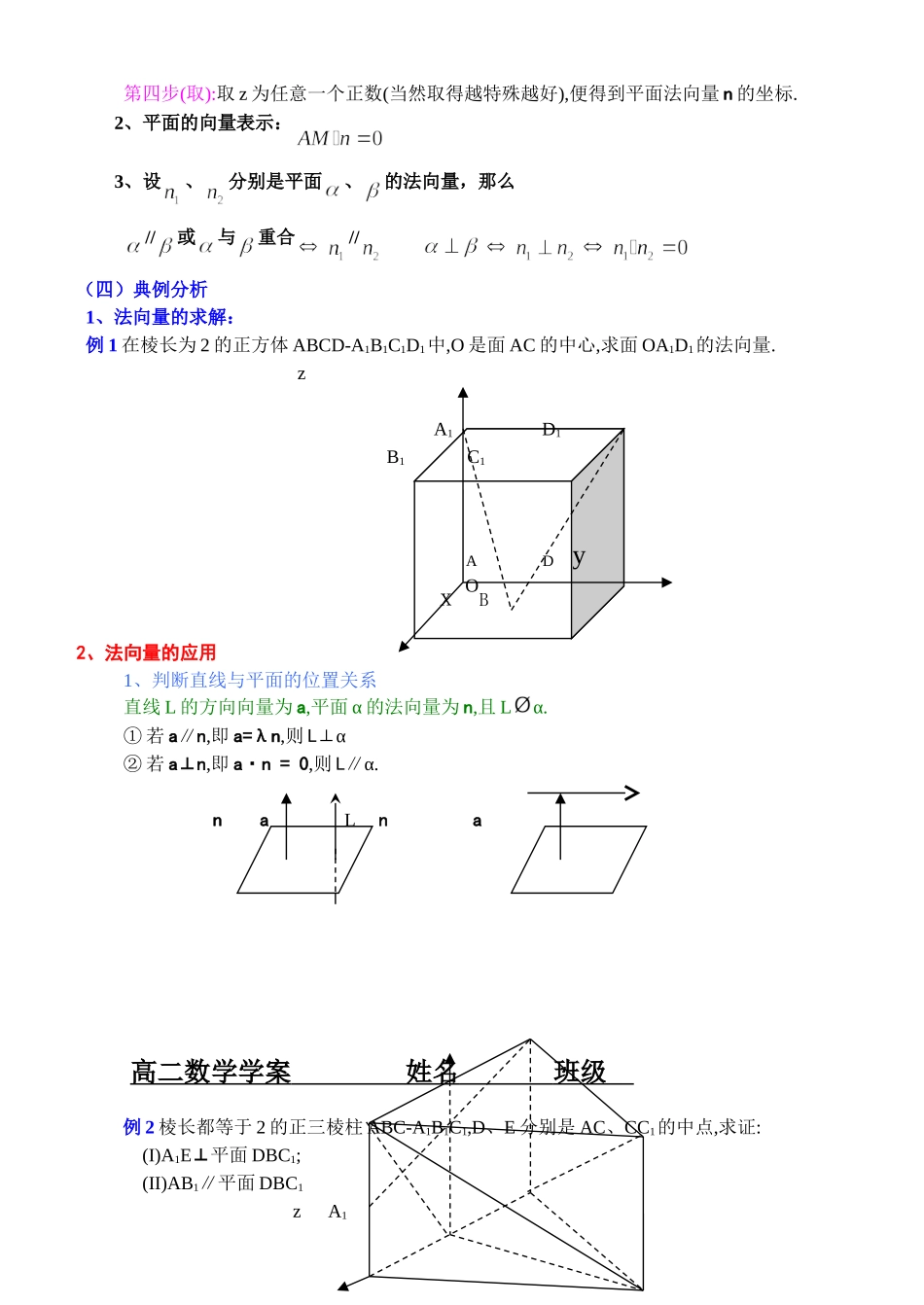
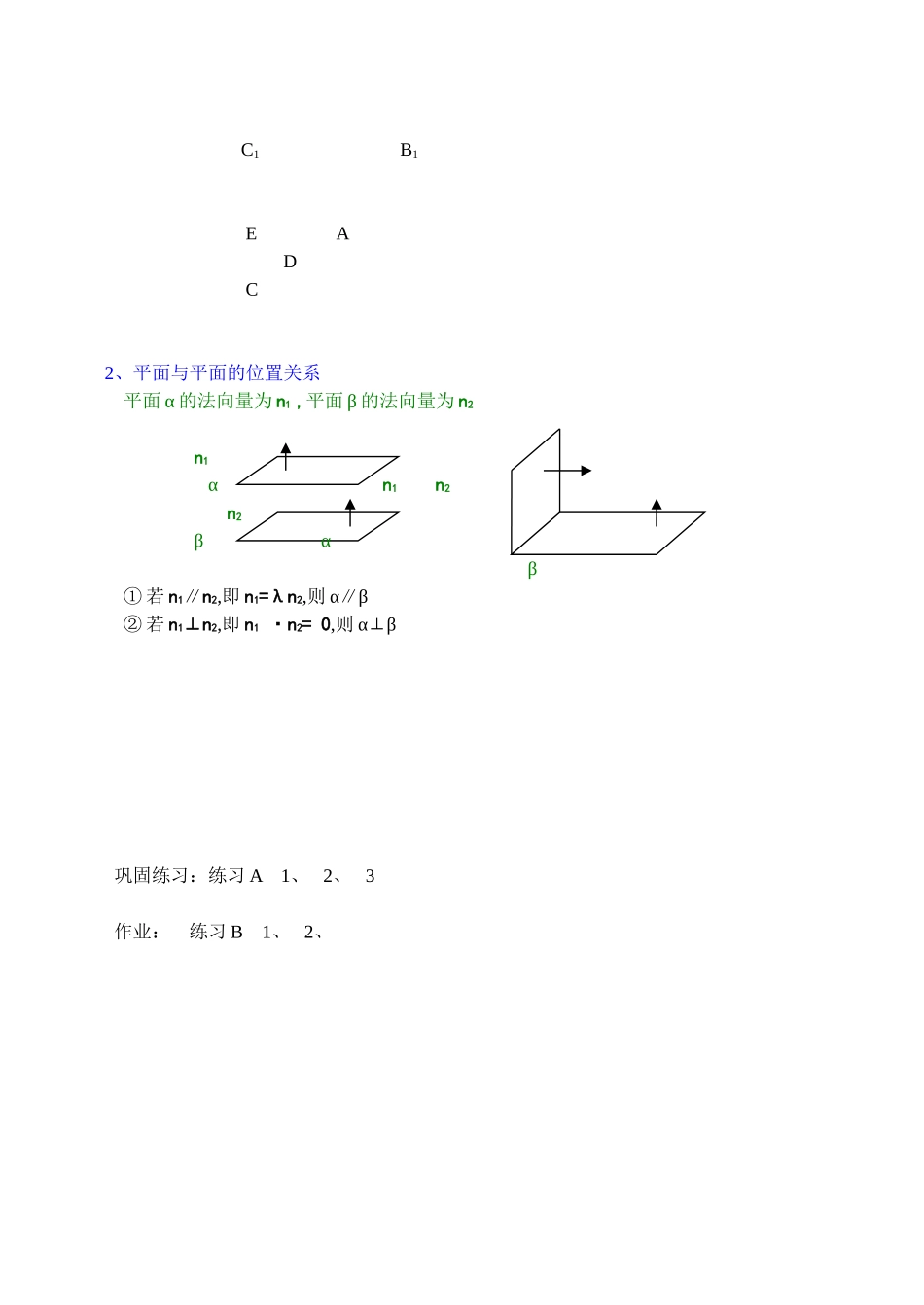
高二数学学案 姓名 班级 高二数学 平面的法向量与平面的向量表示学习目标:1、掌握平面的法向量;会求平面法向量2、利用平面的法向量判定线面、面面的位置关系; 学习重点:法向量的应用 学习过程(一)、预习检测1、设平面 的法向量为(1,2,-2),平面 的法向量为(-2,-4,k),若 ,则 k= ;若 则 k= 。2、已知 ,且 的方向向量为(2,m,1),平面的法向量为(1,1/2,2),则 m= .3、若 的方向向量为(2,1,m),平面 的法向量为(1,1/2,2),且 ,则 m= .4.设 vu,分别是平面 α,β 的法向量,根据下列条件,判断 α,β 的位置关系. (二)、复习:1、 直线 的向量方程: 2、与 , 共面( , 不共线) (三)、引入新课1、平面的法向量及求法如果表示向量 n 的有向线段所在的直线垂直于平面 α,称这个向量垂直于平面 α,记作 n⊥α,这时向量 n 叫做平面 α 的法向量. n在空间直角坐标系中,如何求平面法向量的坐标呢? 如图,设 a=( x1,y1,z1)、b=(x2,y2,z2)是平面 α 内的两个不共线的非零向量,由直线与平面垂直的判定定理知,若 n⊥a且 n⊥b,则 n⊥α.换句话说,若 n·a = 0 且 n·b = 0,则n⊥α.可按如下步骤求出平面的法向量的坐标.第一步(设):设出平面法向量的坐标为 n=(x,y,z).第二步(列):根据 n·a = 0 且 n·b = 0 可列出方程组第三步(解):把 z 看作常数,用 z 表示 x、y.a bA O第四步(取):取 z 为任意一个正数(当然取得越特殊越好),便得到平面法向量 n 的坐标.2、平面的向量表示:3、设、分别是平面、的法向量,那么 //或与重合// (四)典例分析1、法向量的求解:例 1 在棱长为 2 的正方体 ABCD-A1B1C1D1中,O 是面 AC 的中心,求面 OA1D1的法向量. z A1 D1B1 C1A D y x B 2、法向量的应用1、判断直线与平面的位置关系直线 L 的方向向量为 a,平面 α 的法向量为 n,且 Lα. ① 若 a∥n,即 a=λn,则 L⊥α② 若 a⊥n,即 a·n = 0,则 L∥α. n a L n a高二数学学案 姓名 班级 例 2 棱长都等于 2 的正三棱柱 ABC-A1B1C1,D、E 分别是 AC、CC1的中点,求证:(I)A1E⊥平面 DBC1;(II)AB1∥平面 DBC1 z A1 C1 B1 E A D C 2、平面与平面的位置关系平面 α 的法向量为 n1 ,平面 β 的法向量为 n2 n1 α n1 n2 n2 β αβ① 若 n1∥n2,即 n1=λn2,则 α∥β② 若 n1⊥n2,即 n1 ·n2= 0,则 α⊥β巩固练习:练习 A 1、 2、 3作业: 练习 B 1、 2、