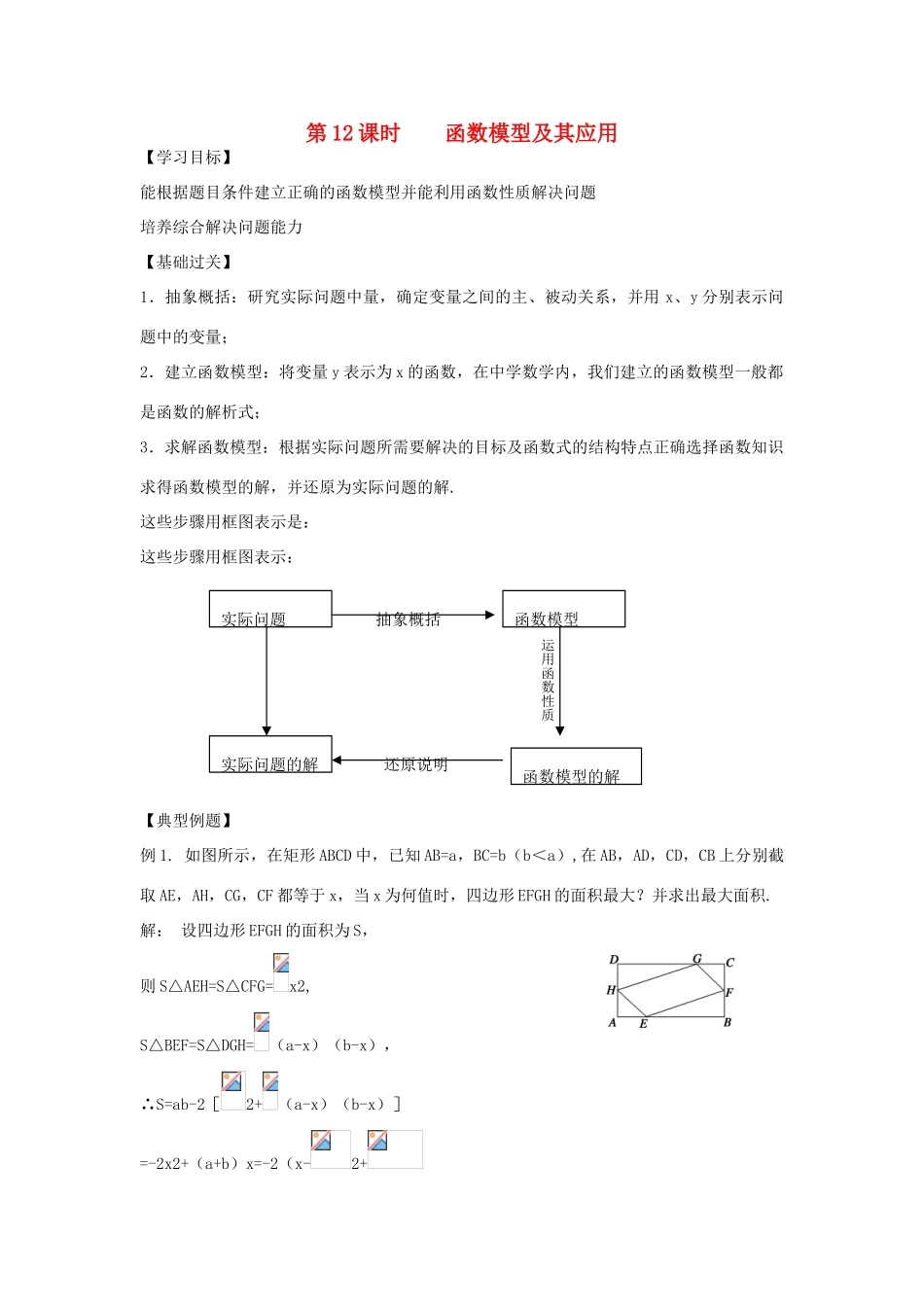
第 12 课时 函数模型及其应用【学习目标】能根据题目条件建立正确的函数模型并能利用函数性质解决问题培养综合解决问题能力【基础过关】1.抽象概括:研究实际问题中量,确定变量之间的主、被动关系,并用 x、y 分别表示问题中的变量;2.建立函数模型:将变量 y 表示为 x 的函数,在中学数学内,我们建立的函数模型一般都是函数的解析式;3.求解函数模型:根据实际问题所需要解决的目标及函数式的结构特点正确选择函数知识求得函数模型的解,并还原为实际问题的解.这些步骤用框图表示是:这些步骤用框图表示:【典型例题】例 1. 如图所示,在矩形 ABCD 中,已知 AB=a,BC=b(b<a),在 AB,AD,CD,CB 上分别截取 AE,AH,CG,CF 都等于 x,当 x 为何值时,四边形 EFGH 的面积最大?并求出最大面积. 解: 设四边形 EFGH 的面积为 S, 则 S△AEH=S△CFG=x2,S△BEF=S△DGH=(a-x)(b-x), ∴S=ab-2[2+(a-x)(b-x)] =-2x2+(a+b)x=-2(x-2+ 实际问题函数模型实际问题的解函数模型的解抽象概括还原说明运用函数性质由图形知函数的定义域为{x|0<x≤b}. 又 0<b<a,∴0<b<,若≤b,即 a≤3b 时, 则当 x=时,S 有最大值; 若>b,即 a>3b 时, S(x)在(0,b]上是增函数, 此时当 x=b 时,S 有最大值为 -2(b-)2+=ab-b2, 综上可知,当 a≤3b 时,x=时, 四边形面积 Smax=, 当 a>3b 时,x=b 时,四边形面积 Smax=ab-b2. 变式训练 1:某商人将进货单价为 8 元的某种商品按 10 元一个销售时,每天可卖出 100 个,现在他采用提高售价,减少进货量的办法增加利润,已知这种商品销售单价每涨 1 元,销售量就减少 10 个,问他将售价每个定为多少元时,才能使每天所赚的利润最大?并求出最大值. 解:设每个提价为 x 元(x≥0),利润为 y 元,每天销售总额为(10+x)(100-10x)元,进货总额为 8(100-10x)元, 显然 100-10x>0,即 x<10, 则 y=(10+x)(100-10x)-8(100-10x)=(2+x)(100-10x)=-10(x-4)2+360 (0≤x<10). 当 x=4 时,y 取得最大值,此时销售单价应为 14 元,最大利润为 360 元. 例 2. 据气象中心观察和预测:发生于 M 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间 t(h)的函数图象如图所示,过线段 OC 上一点 T(t,0)作横轴的垂线 l,梯形 OABC 在直线 l 左侧部分的面积即为 t(h)内沙尘暴所经过的路...