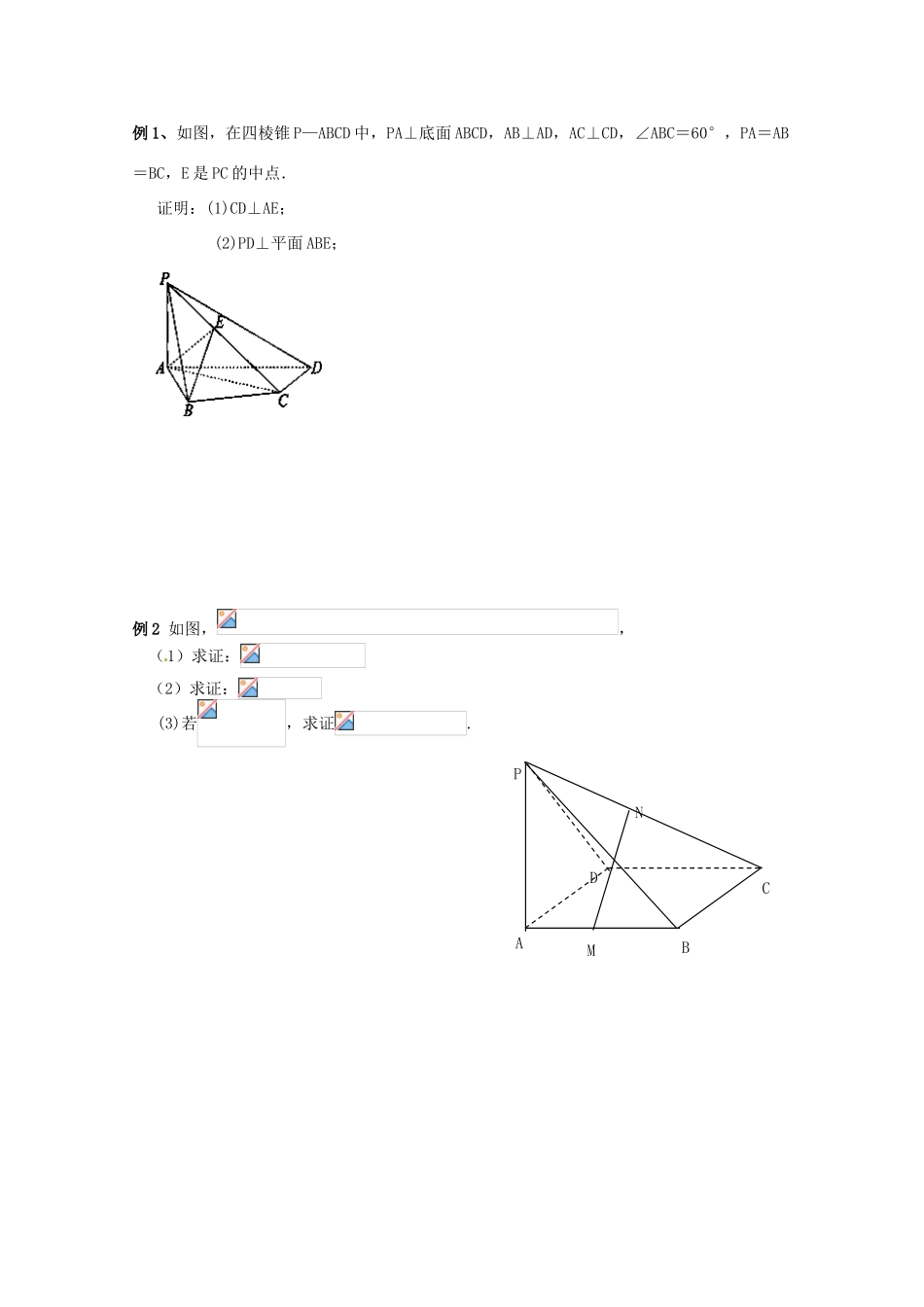
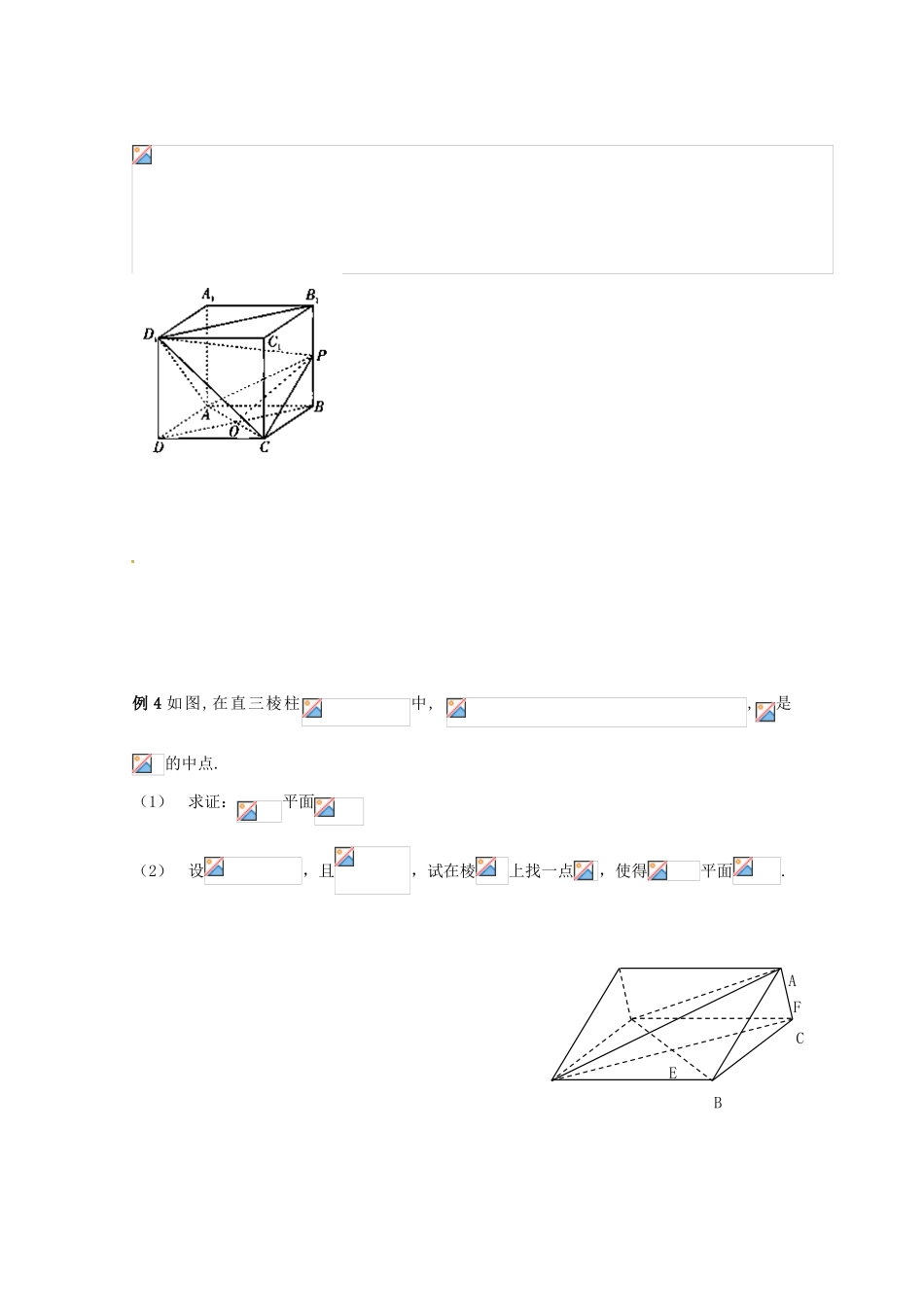
江苏省响水中学 2014 届高考数学一轮复习 第 53-54 课时 直线与平面垂直学案 文【课题】直线和平面垂直【课时】第 53-54 课时复习目标1. 掌握直线和平面垂直的判定定理和性质定理,并能运用它们进行论证和解决有关问题.2.正确理解点到面的距离、线面距离,会利用相关知识论证解决有关问题1.直线与平面垂直的定义: 2.直线与平面垂直的判定定理:3.直线与平面垂直的性质定理:4.点到平面的距离,直线和平面的距离,直线与平面所称的角的概念.1.下列命题中正确的命题有 个① 如果一条直线垂直于一个平面内的无数条直线,那么这条直线与这个平面垂直;②过空间一点有且只有一条直线与已知平面垂直;③一条直线垂直于平面内两条直线,则这条直线垂直于这个平面;④垂直于同一个平面的两条直线平行2. 已知直线 l⊥平面,有以下几个判断:① 若 m⊥l, 则 m∥;② 若 m⊥,则 m∥l ;③ 若 m∥,则 m⊥l;④ 若 m∥l ,则 m⊥.其中正确的是_______.3.已知 AB 是圆 O 的直径,C 是圆 O 上不同于 A、B 的任意一点,PA 垂直于圆 O 所在的平面,则△PAB、△PAC、△ABC、△PBC 中,共有 个直角三角形.4.在矩 ABCD 中,AB=3,BC=4,PA⊥面ABCD,PA=1,则 P 到对角线 BD 的距离为______________ .5.在空间四边形 ABCD 中(1)若 AB=AC=AD,则 A 在面 BCD 上的射影为△BCD 的 心.(2)若 AB=AC=AD,且∠BCD=9 0°,则 A 在面 BCD 上的射影所在位置是 . (3)若 AB、AC、AD 两两垂直,则 A 在面 BCD 上的射影为△BCD 的 心.6. 设 ,是两条不同的直线,是一个平面,则下列命题正确的是____________(A)若,,则 (B)若,,则(C)若,,则 (D)若,,则例 1、如图,在四棱锥 P—ABCD 中,PA⊥底面 ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E 是 PC 的中点.证明:(1)CD⊥AE; (2)PD⊥平面 ABE; 例 2 如图,, (1)求证: (2)求证: (3)若,求证.ADNBCPM例 4 如图,在直三棱柱中, ,是的中点.(1)求证:平面(2)设,且,试在棱上找一点,使得平面.ABCEF直线和平面垂直反馈练习1.在空间四边形中,分别为的中点,为对角线的中点,若,则 .2 . 设依 次 是 四 面 体的 棱的 中 点 , 且,则 .3.如图 PA矩形 ABCD 所在平面,M、N 分别是 AB 和 PC 中点.(1)求证:MNCD;(2)若,求证:MN平面 PCD4.如图 SA⊥面 ABC,∠ABC=90°,AE⊥SB,且 SB∩AE=E,AF⊥SC,且 AF∩SC=F,求证:(1) AE⊥面 SBC;(2) SC⊥EF5. 如图,已知长方体的底面 ABCD 是正方形,E 为线段 AD1的中点,F 为线段 BD1的中点.(1)求证:EF//平面 ABCD; (2)设 M 为线段 C1C 的中点,当的比值为多少时,DF平面 D1MB? 说明理由. DABCPMNSABCFEA1D1C1B1CBDAEFM