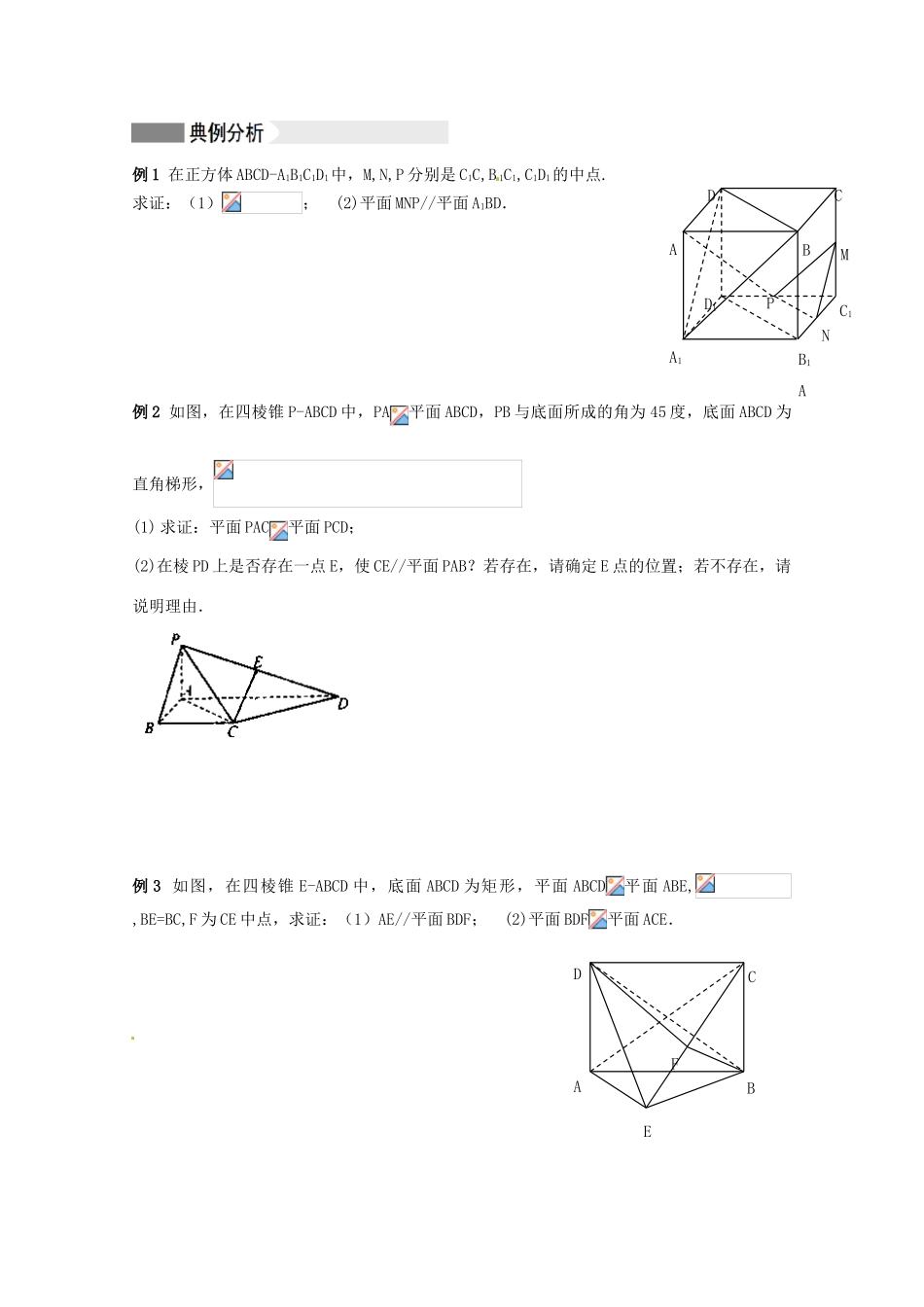
江苏省响水中学 2014 届高考数学一轮复习 第 55-56 课时 平面与平面的位置关系学案 文【课题】平面与平面的位置关系【课时】第 55-56 课时复习目标1. 了解两个平面的位置关系,理解面面平行与垂直的判定定理及性质定理,会证明面面平行与垂直2. 熟练运用“直线与直线”、“直线与平面”、“平面与平面”之间的相互转化思想 ,证明或解决线线、线面、面面之间的平行与垂直问题。3.了解二面角及其平面角、平面与平面距离等概念,能在长方体模型中进行说明。1、平面与平面平行的判定定理:__________________________________________________2、平面与平面平行的性质定理____________________________________________________3、两个平面垂直的定 义:________________________________________________________4、平面与平面的垂直的判定定理:_______________________________________________1.直线 是平面的一条斜线,则过 和平面垂直的平面有 个.2 . 若 平 面// 平 面, 直 线, 直 线, 那 么 直 线的 位 置 关 系 是 .3.给出条件:(1)(3)(其中为不同直线,为不同平面),则上述条件能推出的是__________(填序号).4.ABCD 是正方形,P 为平面 ABCD 外一点,且 PA⊥平面 ABCD,则平面 PAB,平面 PBC,平面PDC,平面 PAD,平面 ABCD 这五个面中,互相垂直的平面有 对.5.如图,已知 PA菱形 ABCD 所在的平面,M 是 PC 上的一动点,当 M 满足_______________时,平面 MDB平面 ABCD.6.设直线 l 和平面,且,给出 如 下三个式子:①,②,③.从中任取两个作为条件,余下一个作为结论,在构成的命题中,写出一个你认为正确的一个命题 .例 1 在正方体 ABCD-A1B1C1D1中,M,N,P 分别是 C1C,B 1C1,C1D1的中点.求证:(1); (2)平面 MNP//平面 A1BD.例 2 如图,在四棱锥 P-ABCD 中,PA平面 ABCD,PB 与底面所成的角为 45 度,底面 ABCD 为直角梯形,(1) 求证:平面 PAC平面 PCD;(2)在棱 PD 上是否存在一点 E,使 CE//平面 PAB?若存在,请确定 E 点的位置;若不存在,请说明理由.例 3 如图,在四棱锥 E-ABCD 中,底面 ABCD 为矩形,平面 ABCD平面 ABE,,BE=BC,F 为 CE 中点,求证:(1)AE//平面 BDF; (2)平面 BDF平面 ACE.ADCC1B1AD1A1NPBMDAEBCF例 4 如图所示,在直三棱柱 ABC-A1B1C1中,AB=BB1,D 为 AC ...