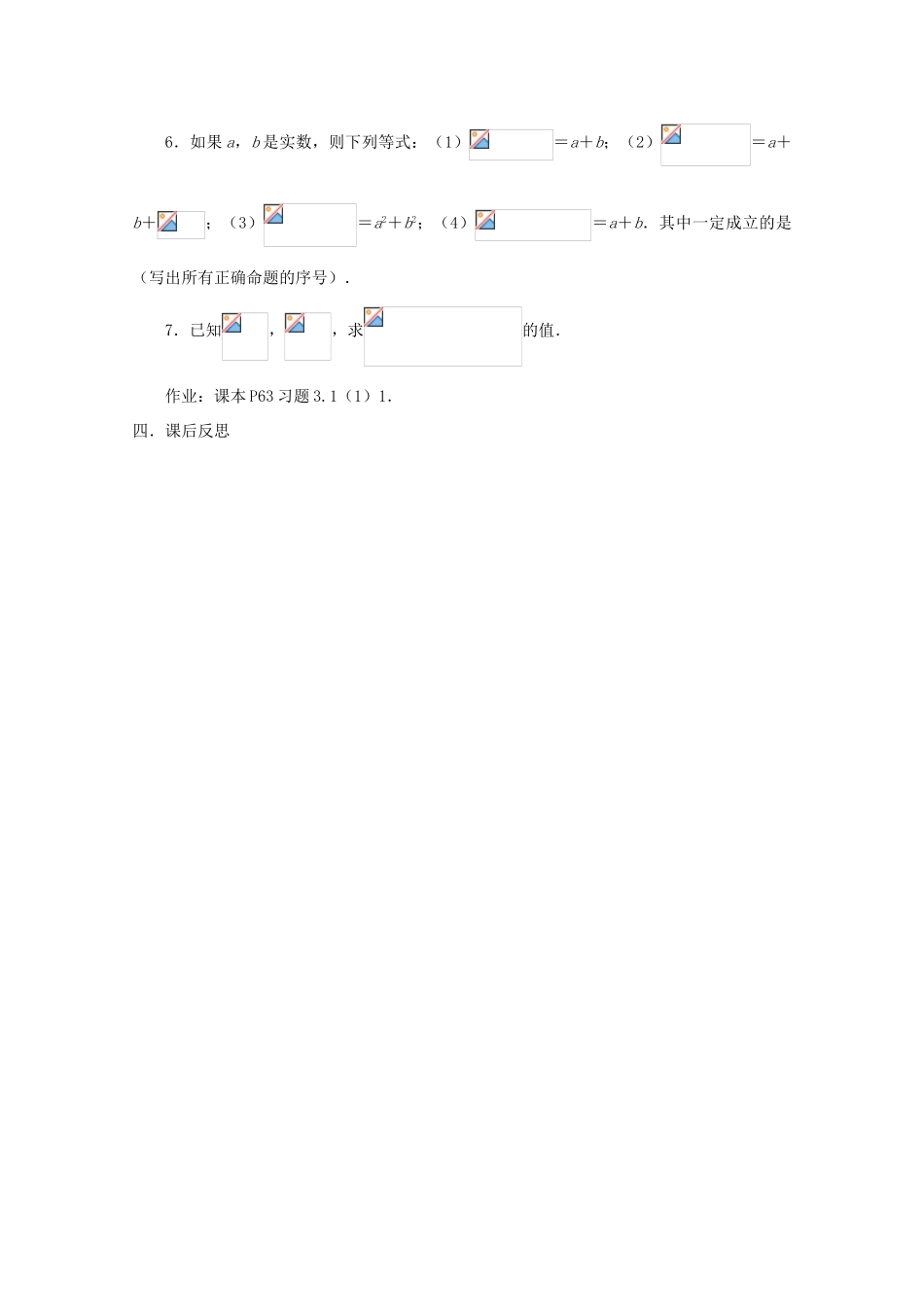
章节与课题2
1 分数指数幂(1)课时安排1 课时本课时学习目标或学习任务理解根式的概念及 n 次方根的性质．本课时重点难点或学习建议重点：根式的运算．难点：根式性质的理解．一．自学准备与知识导学：1
复习平方根、立方根的定义：（1）如果 x2＝a，那么 x＝ （2）如果 x3＝a，那么 x＝ 2．类比得出 n 次实数方根的概念二．学习交流与问题研讨：1．n 次实数方根的概念如果 xn＝a，那么 x＝ （n 为正整数，且 n≥2）注：（1）在实数范围内，正数的奇次方根是一个___数，负数的奇次方根是一个___数，零的奇次方根是___，即任一个实数都有且只有___个奇次方根,记作 x＝____．（2）在实数范围内，正数的偶次方根是_______________________，正数 a 的正的偶次方根记作 x＝____，正数 a 的负的偶次方根记作 x＝____，它们可以合并记作 x＝____，零的偶次方根是____，负数的偶次方根________．（3）当 a≥0 时，对于任意不小于 2 的整数 n，的值存在且惟一，表示 a 的 n 次算术根；当 a＜0 时，当且仅当 n 为奇数（n＞1）时，才有意义．例 1 求值．（1） （2） （3） （4） （5） （6） （7）总结：根式的性质．2．根式的性质．（1）＝_____．（2） ＝_________
例 2 计算下列各式的值．（1）（2）（3）三．练习检测与拓展延伸 1
教材第 62 页: 练习 12．（1）25 的平方根是 ；（2）27 的立方根是 ； （3）16 的四次方根是 ；（4）－32 的五次方根是 ；（5）a6的六次方根是 ；（6）0 的 n 次方根是 ．3
求下列各式的值4．下列说法：（1）正数的 n 次方根是正数；（2）负数的 n 次方根是负数；（3）0 的 n次方根是 0；（4）是无理数．其中正确的
