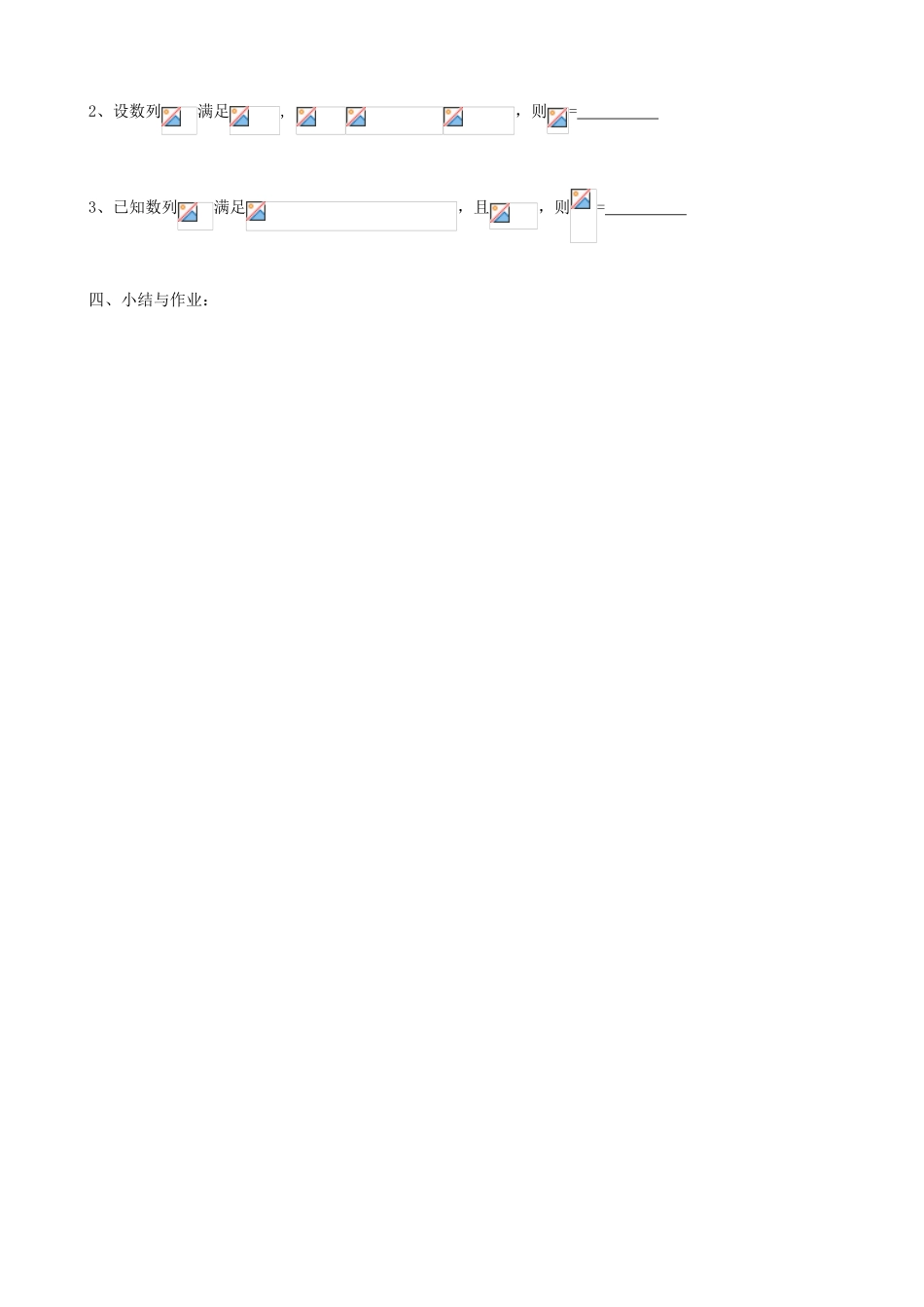
数列的概念 2一、学习目标:1、了解数列的递推公式;2.掌握数列通项公式的写法.二、预习效果回顾: 一般地, ,那么这个公式叫做这个数列的通项公式.1.在数列中,若,则= .2.已知数列的前五项分别为 1,4,9,16,25,… ,,则它的一个通项公式为 .3、已知数列的前五项分别为-1,3,-5,7,-9… ,则它的一个通项公式为 .4、在数列中,若,则数列中的最小项为 三、例题例 1. 写出下列数列的一个通项公式:(1),,,,…; (2),,,,…;(3)1,3,1,3,…; (4)1,3,6,10,15,…(5) 1,2,4,8,16… (6)9,99,999,9999,99999,…练习:1、已知数列的前五项分别为 2,5,10,17,26,… ,,则它的一个通项公式为 .2.数列,,,,,,...,的一个通项公式为____________.3、已知数列的前五项分别为 1,11,111,1111,11111,… ,,则它的一个通项公式为 .4、.数列 ,, ,, ,,的一个通项公式是____________.例 2、已知数列的第一项(或前几项),且任一项与它的前一项(或前几项)间的关系可以用一个公式来表示,这个公式就叫做这个数列的递推公式. 利用递推公式也可以给出数列;下图的三角形称为谢宾斯基(Sierpinski)三角形。黑色的三角形依次 是一个数列的前 5 项,数数他们的个数.思考: 你对这个数列的项之间的关系的发现是 (1)已知数列满足,写出这个数列的前 5 项,并猜想它的通项公式.(2)已知数列中,,则 = (3)设数列满足, ,则= .4、已知数列满足,,,试写出数列的前 5 项.练习1、已知数列的前五项分别为,则它的一个通项公式为 2、设数列满足, ,则= 3、已知数列满足,且,则= 四、小结与作业: