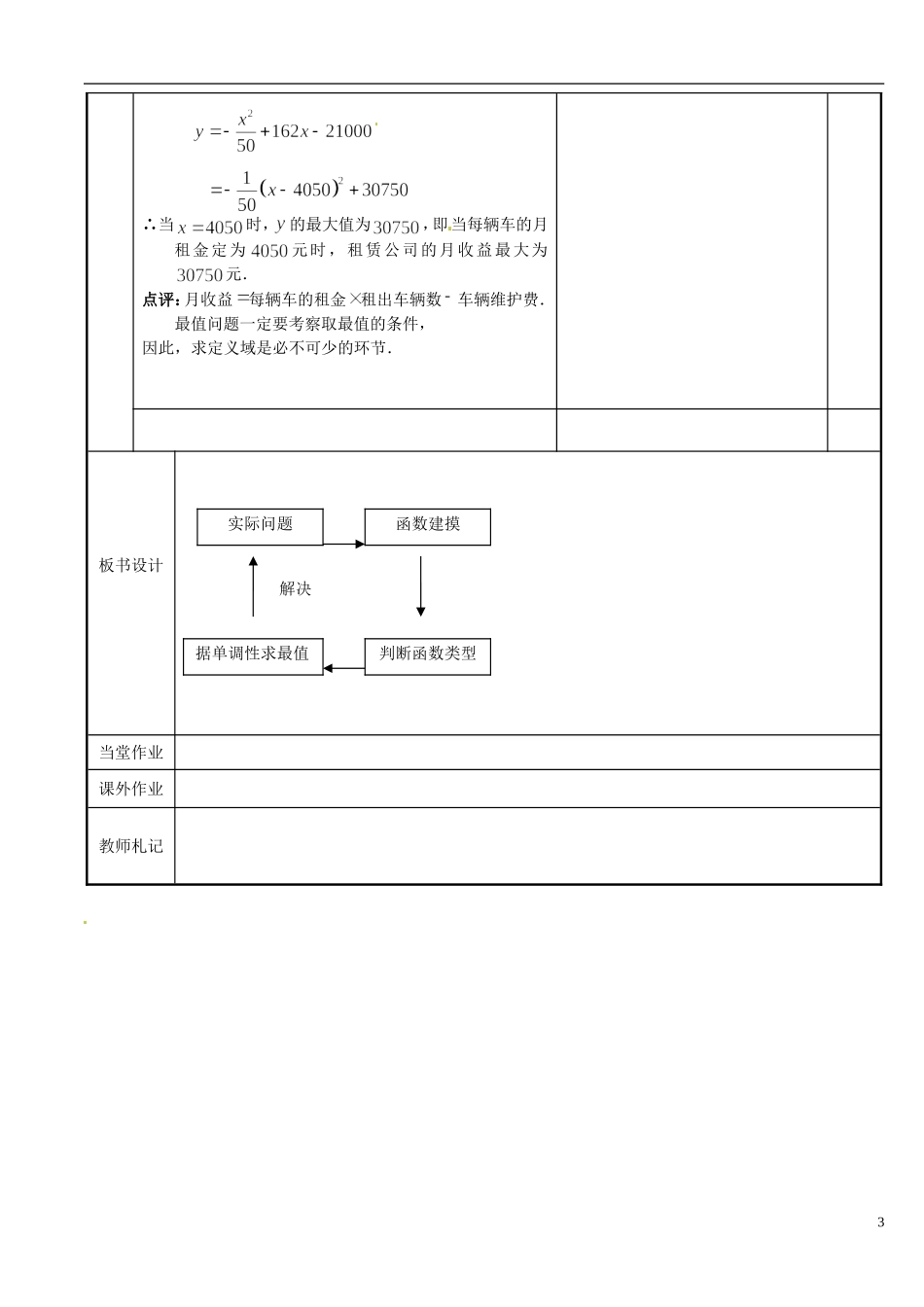
江苏省新沂市第二中学 2014-2015 学年高中数学 第 42 课时 函数的模型教案 苏教版必修 1课题第三十五课时函数模型及其应用(3)课型新 授课教学目标1.根据条件题意写出满足题意的函数;2. 能够根据一次函数、二次函数的单调性来求出所写函数的最大值和最小值.重点二次函数的单调性来求出所写函数的最大值和最小值.难点二次函数的单调性来求出所写函数的最大值和最小值.教法讲授法、讨论法、探究法教学过程教 学 内 容 个案调整教师主导活动学生主体活动 自学评价11.一次函数求最值主要是利用它的 单调性 ;2 2 求最值也是要利用它的单调性,一般我们都先 配方 .3.3 什 么 函 数 求 最 值 都 要 注 意 能 够 取 到 最 值 的 条 件 .例如 定义域 等 . 【精典范例】例 1:在经济学中,函数的边际函数定义为=.某公司每月最多生产台报警 系 统 装 置 , 生 产台 () 的 收 入 函 数( 单 位 : 元 ), 其 成 本 函 数 为(单位:元),利润是收入 与成本之差.(1)求利润函数及边际利润函数;(2)利润函数与边际利润函数是否具有相同的最大值?【解】由题意知,,且.(1)= 追踪训练一1.冬季来临,某商场进了一批单价为元的电暖保,如 果 按元一个销售,能卖个;若销售单价每上涨 元,销售量就减少 个,要获得最大利润时,电暖保的销售单价应该为多少?提示:设单价为元,利润为元,则所 以 当时 ,的 最 大 值 为.1 (2) 当或时, 的最大值为 (元).因 为是 减 函 数 , 所 以 当时 , 的最大值为 (元).因此,利润函数与边际利润函数不具有相同的最大值.2:某租赁 公司拥有汽车辆.当每辆车的月租金为元时,可全部租出.当每辆车的月租金每增加元时,未出租的车将会增加一辆.租出的车每辆每月需要维护费元,未租出的车每辆每月需要维护费元.(1)当每辆车的月租金定为时,能租出多少辆车?(2)当每辆车的月租金定为多少元时?租赁公司的月收益最大?最大月收益是多少?【解】(1)当每辆车的月租金定为时,未租出的车辆数为,∴租出了辆车.(2)设每辆车的月租金为元,则租赁公司月收益为整理后得2.某商品 在近天内每件的销售价格(元)与时间 (天)的函数关系是,该商品的日销售量(件)与时间(天)的函数关系是,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是天中的第几天.解:第天,日销售金额最大为元.2 ∴当时, 的最大值为,即...