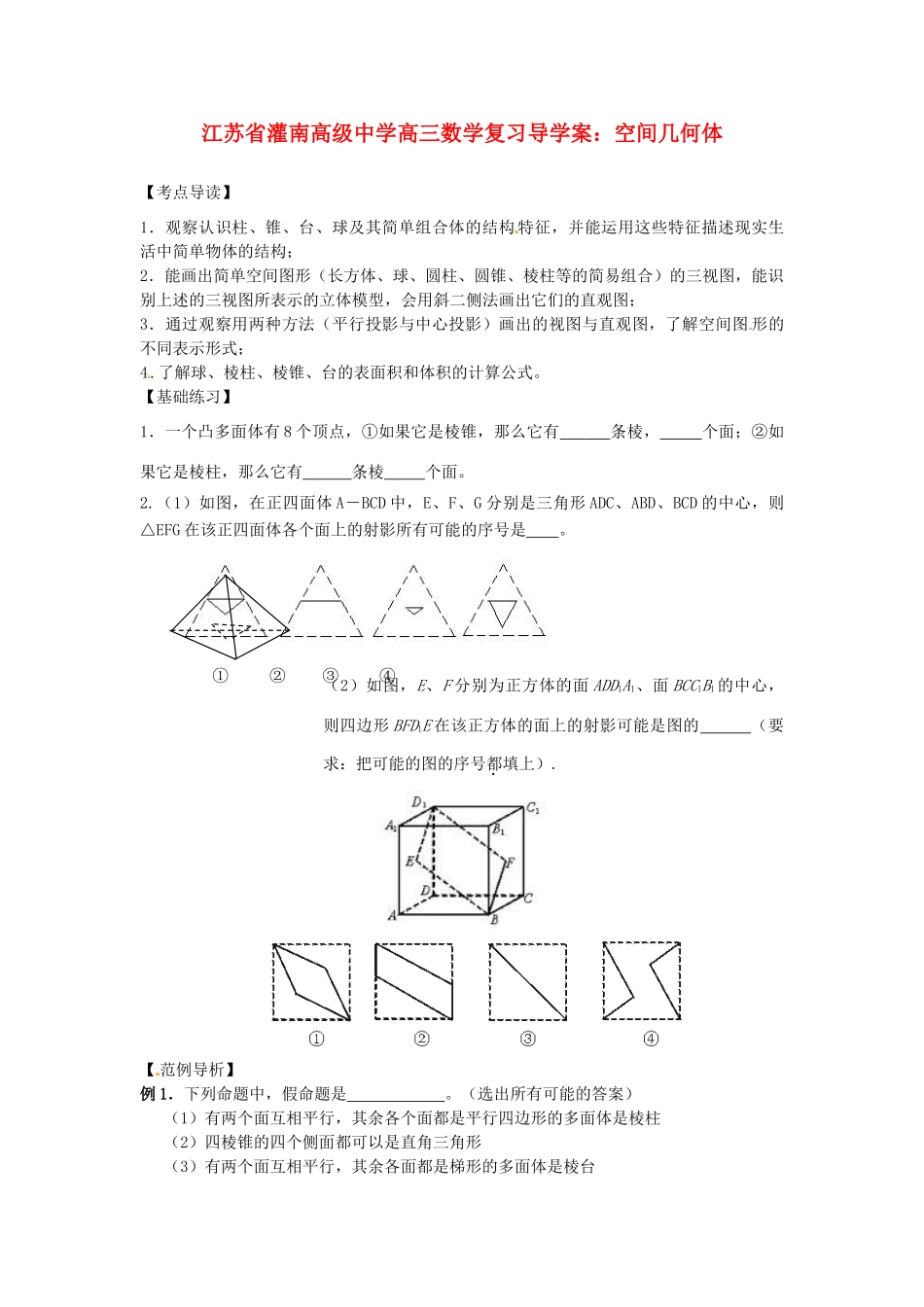
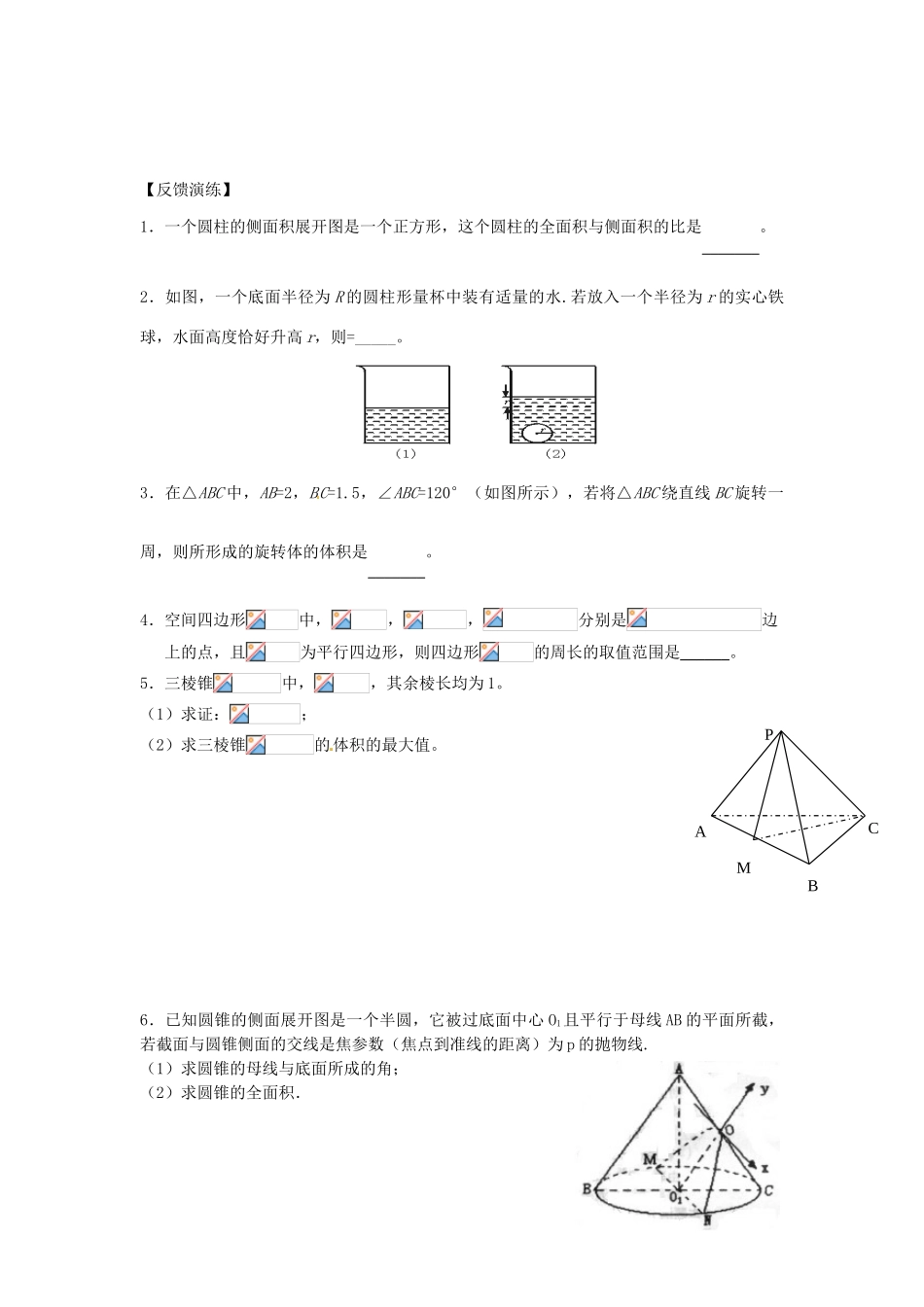
江苏省灌南高级中学高三数学复习导学案:空间几何体【考点导读】1.观察认识柱、锥、台、球及其简单组合体的结构 特征,并能运用这些特征描述现实生活中简单物体的结构;2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述的三视图所表示的立体模型,会用斜二侧法画出它们的直观图;3.通过观察用两种方法(平行投影与中心投影)画出的视图与直观图,了解空间图 形的不同表示形式;4.了解球、棱柱、棱锥、台的表面积和体积的计算公式。【基础练习】1.一个凸多面体有 8 个顶点,①如果它是棱锥,那么它有 条棱, 个面;②如果它是棱柱,那么它有 条棱 个面。2.(1)如图,在正四面体 A-BCD 中,E、F、G 分别是三角形 ADC、ABD、BCD 的中心,则△EFG 在该正四面体各个面上的射影所有可能的序号是 。(2)如图,E、F 分别为正方体的面 ADD1A1、面 BCC1B1 的中心,则四边形 BFD1E 在该正方体的面上的射影可能是图的 (要求:把可能的图的序号都填上).【 范例导析】例 1.下列命题中,假命题是 。(选出所有可能的答案)(1)有两个面互相平行,其余各个面都是平行四边形的多面体是棱柱(2)四棱锥的四个侧面都可以是直角三角形(3)有两个面互相平行,其余各面都是梯形的多面体是棱台 ①②③④(4)若一个几何体的三视图都是矩形,则这个几何体是长方体例 2.是正△ABC 的斜二测画法的水平放置图形的直观图,若的面积为,那么△ABC 的面积为_______________。【反馈演练】1.一个圆柱的侧面积展开图是一个正方形,这个圆柱的全面积与侧面积的比是_______。2.如图,一个底面半径为 R 的圆柱形量杯中装有适量的水.若放入一个半径为 r 的实心铁球,水面高度恰好升高 r,则=_____。3.在△ABC 中,AB=2,BC=1.5,∠ABC=120°(如图所示),若将△ABC 绕直线 BC 旋转一周,则所形成的旋转体的体积是_______。4.空间四边形中,,,分别是边上的点,且为平行四边形,则四边形的周长的取值范围是______。5.三棱锥中,,其余棱长均为 1。(1)求证:;(2)求三棱锥的体积的最大值。6.已知圆锥的侧面展开图是一个半圆,它被过底面中心 O1且平行于母线 AB 的平面所截,若截面与圆锥侧面的交线是焦参数(焦点到准线的距离)为 p 的抛物线.(1)求圆锥的母线与底面所成的角;(2)求圆锥的全面积. PABCM第 4 课 空间中的垂直关系【考点导读】1.掌握直线与平面、平...