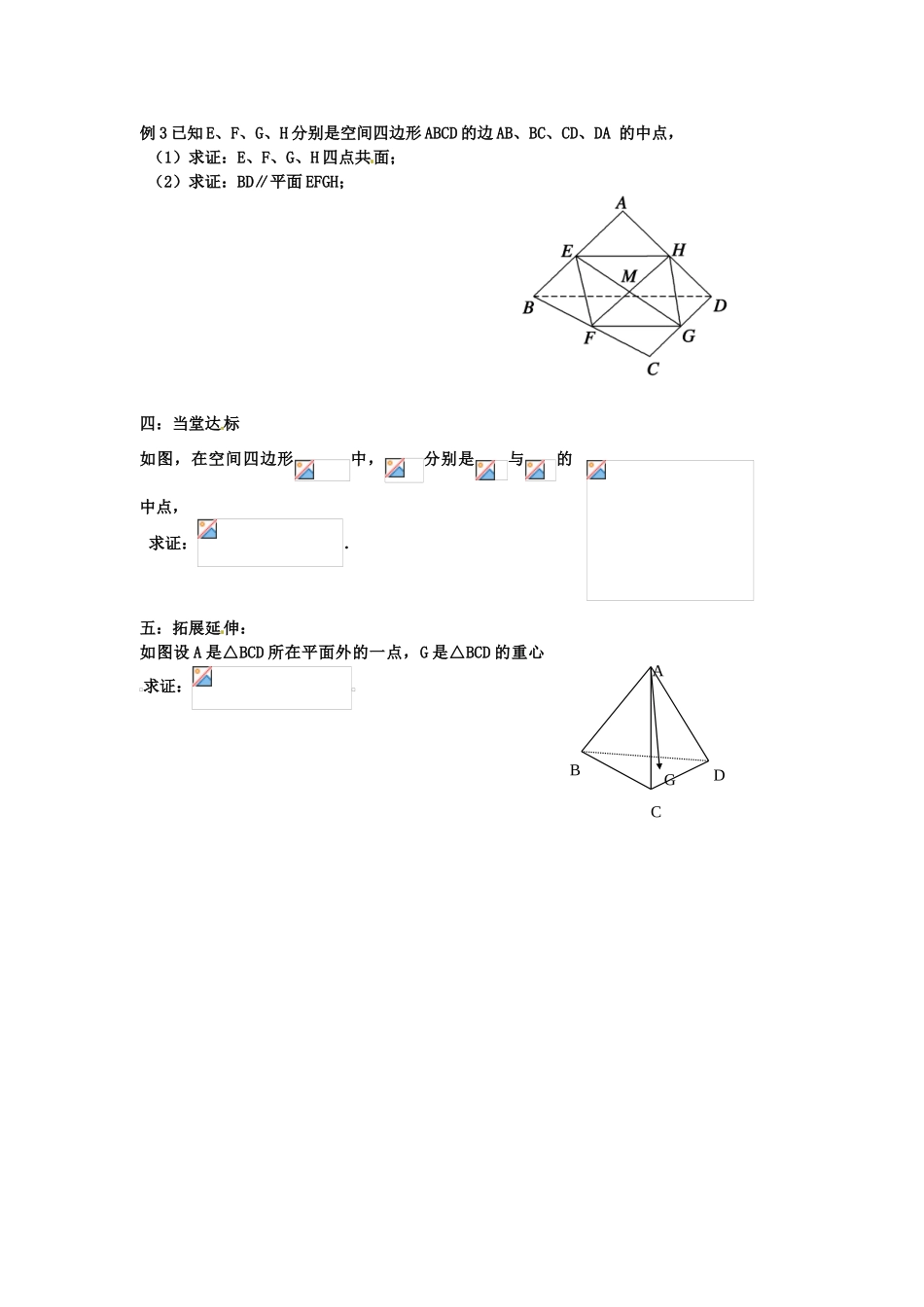
江苏省灌南高级中学高三数学复习导学案:空间直线的方向向量和平面的法向量一:教学目的:1.理解空间向量的概念,掌握空间向量的加法、减法和数乘运算2.用空间向量的运算意义、运算律以及共线、共面向量定理解决立几问题 二:自主导学问题 1:空间向量的相关概念有哪些?(1)向量的基本要素:(2)向量的表示:(3)向量的长度:(4)特殊的向量: (5)相等的向量: (6)平行向量(共线向量): 问题 2 平面向量的加减法,数与向量的乘积及其各运算的坐标表示和性质如下表,其适用于空间向量吗? 有何联系与区别?运算类型几何方法坐标方法运算性质向量的加法1 平行四边形法则2 三角形法则向量的减法三角形法则向量的1是一个向量,满足:2>0 时,与同向;<0 时,与异向;乘法=0 时, =0∥问题 3:共线向量 共面向量 注:“空间任意两个向量都是共面向量,所以它们可用同一平面内的两条有向线段表示。 因此凡是只涉及空间任意两个向量的问题,平面向 量中有关结论仍适用于它们”这句话正确吗?为什么?问题 4:平面共线向量定理?空间共线向量定理 空间共面向量定理 三:典例分析:题型一 空间向量的线性运算例 2 已知空间四边形,连结,设分别是的中点,化简下列各表达式,并标出化简结果向量:(1); (2); (3).题型二 共线、共面向量定理的应用BACDG例 3 已知 E、F、G、H 分别是空间四边形 ABCD 的边 AB、BC、CD、DA 的中点, (1)求证:E、F、G、H 四点共面; (2)求证:BD∥平面 EFGH;四:当堂达标如图,在空间四边形中,分别是与的中点,求证:.五:拓展延伸:如图设 A 是△BCD 所在平面外的一点,G 是△BCD 的重心求证: