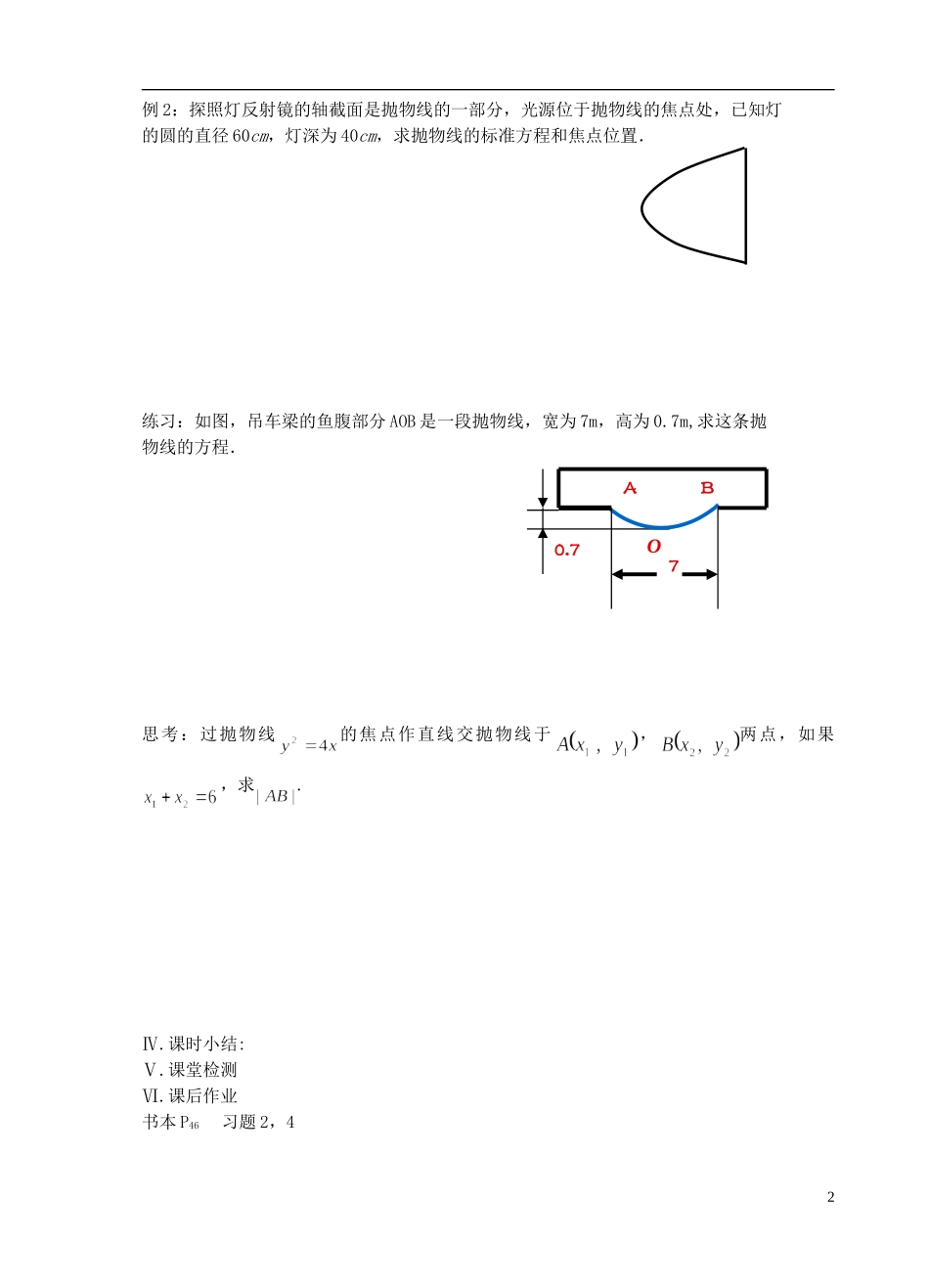
高中数学教学案第二章 圆锥曲线与方程第 12 课时 抛物线的几何性质(1)教学目标:1. 掌握抛物线的范围、对称性、顶点、离心率等几何性质;2. 能根据抛物线的几何性质对抛物线方程进行讨论,在此基础上列表、描点、画抛物线图形;3. 在对抛物线几何性质的讨论中,注意数与形的结合与转化.教学重点: 抛物线的几何性质及其运用教学难点: 抛物线几何性质的运用教学过程:Ⅰ.问题情境抛物线()的取值范围是什么?对称性是怎样的? 有顶点吗?Ⅱ.建构数学 抛物线的几何性质: 1.范围: 2.对称性: 3.顶点: 4.渐进线: 5.离心率:Ⅲ.数学应用例 1:求顶点在原点,焦点 F 为(5,0)的抛物线的方程. 练习:根据下列条件,求抛物线的标准方程: (1)顶点在原点,焦点 F 为(0,4);(2)顶点在原点,关于 x 轴对称,并且经过点 M(-5, 4).1例 2:探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯的圆的直径 60cm,灯深为 40cm,求抛物线的标准方程和焦点位置.练习:如图,吊车梁的鱼腹部分 AOB 是一段抛物线,宽为 7m,高为 0.7m,求这条抛物线的方程.思考:过抛物线的焦点作直线交抛物线于,两点,如果,求.Ⅳ.课时小结:Ⅴ.课堂检测Ⅵ.课后作业书本 P46 习题 2,42O7AB0.71. 根据下列条件,求抛物线的标准方程: (1)顶点在原点,焦点 F 为(0,-5);(2)顶点在原点,关于 y 轴对称,且经过点 M (4, -3).2.已知抛物线的顶点在原点,关于 y 轴对称,且焦点焦点在直线 x-y+2=0 上,求此抛物线的方程.3. 3