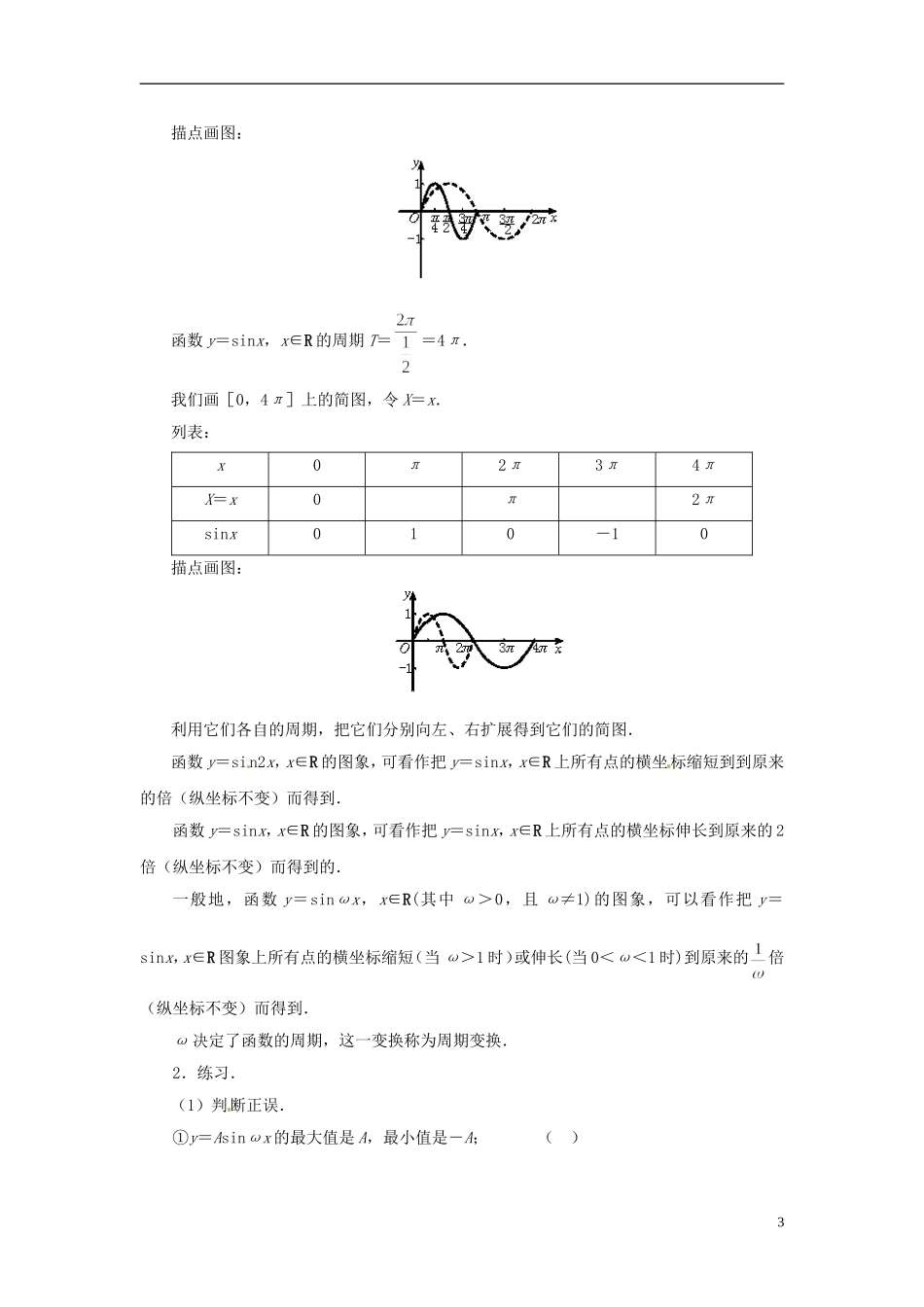
江苏省连云港灌云县第一中学高中数学 1.3.3 函数 y=Asin(ωx+φ)的图象(1)教案 新人教 A 版必修 1教学目标:结合具体实例,了解的实际意义,能借助计算器或计算机画出该函数的图象,研究参数对函数图象变化的影响,会用五点法画出函数的简图.教学重点:1. 函数的图象以及参数对函数图象变化的影响;2.周期变换与振幅变换.教学难点:理解振幅变换和周期变换的规律.教学方法: 启发引导式.教学过程:一、问题情境在现实生活中,我们常常会遇到形如 y=Asin(ωx+ )的函数解析式(其中 A,ω, 都是常数).下面我们讨论函数 y=Asin(ωx+ ),x∈R 的简图的画法.二、学生活动小组合作,列表,描点,讨论.教师适当引导,得到画简图的一般步骤,并取名“五点作图法”,五点作图法的关键是描出图象在一个周期内起关键作用的五个点,它们是使函数取得最大值、最小值的点以及曲线与 x 轴的交点,找出它们的方法是令分别取,进而求出相应的五个点的坐标.三、数学运用首先我们来看形如 y=Asinx,x∈R 的简图如何来画?1.例题.例 1 画出函数 y=2sinx,x∈R,y=sinx,x∈R 的简图.1解 画简图,我们用“五点法”. 这两个函数都是周期函数,且周期为 2π.∴我们先画它们在[0,2π]上的简图.列表:x0π2πsinx010-102sinx[020-20sinx00-0描点画图:然后利用周期性,把它们在[0,2π]上的简图向左、右分别扩展,便可得到它们的简图.请同学们观察它们之间的关系:y=2sinx 图象可看作把 y=sinx,x∈R 上所有点的纵坐标伸长到原来的 2 倍而得(横坐标不变).y=sinx 图象可看作把 y=sinx,x∈R 上所有点的纵坐标缩短到原来的倍而得(横坐标不变).一般地,函数 y=Asinx,x∈R(其中 A>0 且 A≠1)的图象,可以看作把正弦曲线上所有点的纵坐标伸长(当 A>1 时)或缩短(当 0<A<1 时)到原来的 A 倍(横坐标不变)而得到.A 称为振幅,这一变换称为振幅变换.例 2 画出函数 y=sin2x,x∈R y=sinx,x∈R 的简图.解 函数 y=sin2x,x∈R 的周期 T==π.我们先画在[0,π]上的简图.令 X=2x,那么 sinX=sin2x.列表:x0πX=2x0π2πsinx010-102描点画图:函数 y=sinx,x∈R 的周期 T==4π.我们画[0,4π]上的简图,令 X=x.列表:x0π2π3π4πX=x0π2πsinx010-10描点画图:利用它们各自的周期,把它们分别向左、右扩展得到它们的简图.函数 y=sin2x...