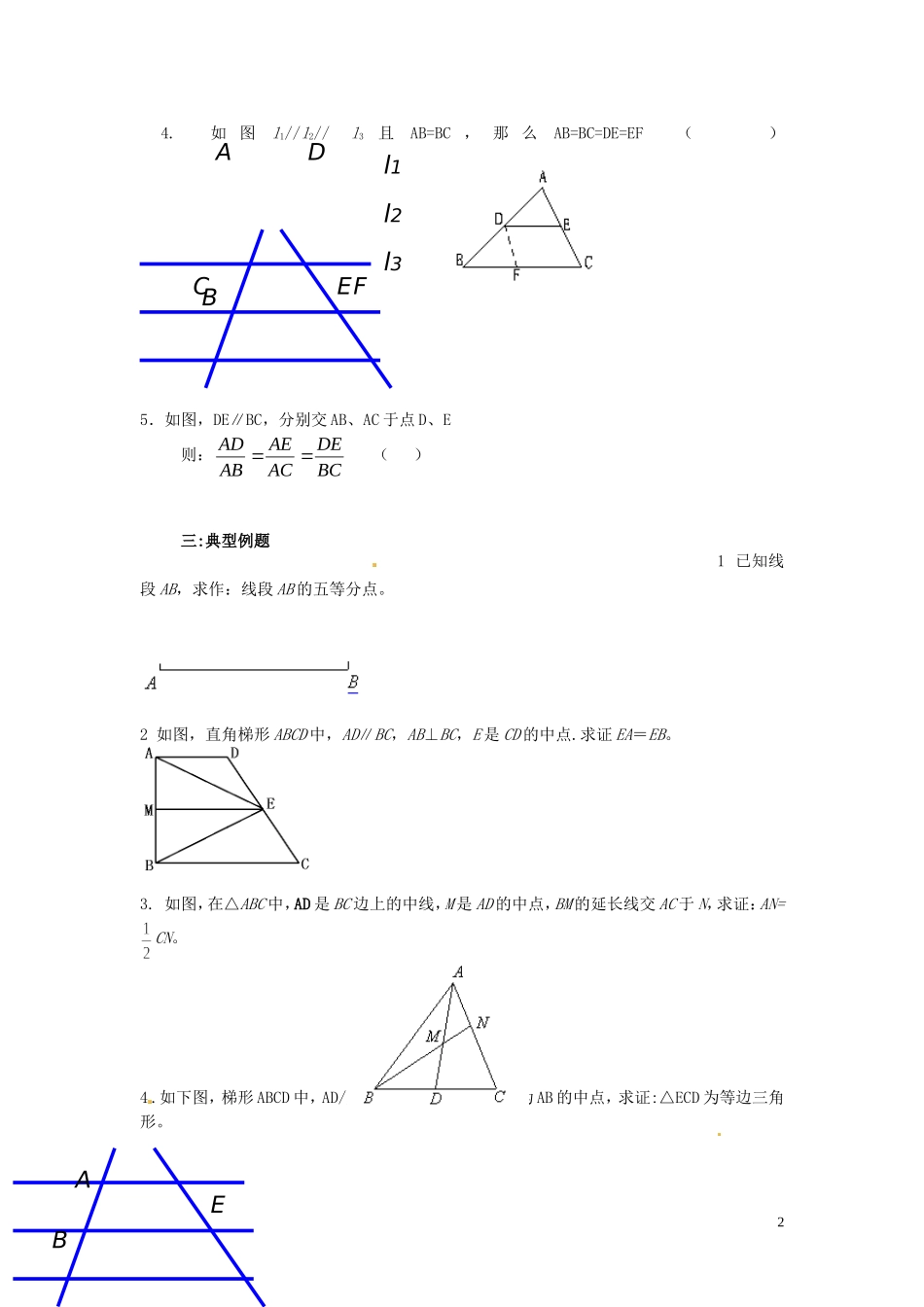
DBEF河北省唐山市开滦第二中学高中数学 1.1-1.2 平行线等分线段定理与学案 新人教 A 版选修 4-1【学习目标】1.探索并理解平行线分线段定理的证明过程;2.能独立证明平行线分线段定理的推论 1、推论 2;3.平行线分线段成比例定理与推论的区别4.能应用定理和推论解决相关的几何计算问题和证明问题【重点难点】 能应用定理和推论解决相关的几何计算问题和证明问题【学习内容】一:知识梳理1.平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段 推论 1:经过三角形一边的中点与另一边平行的直线必 推论 2:经过梯形一腰的中点,且与底边平行的直线 2.三条平行线截两条直线,所得的对应线段 推论:平行于三角形的一边,并且和其他两边相交的直线。所截得的三角形的三 边与原三角形的三边 二:基本技能:判断下列命题是否正确1. 如图△ABC 中点 D、E 三等分 AB,DF∥EG∥BC,DF、EG 分别交 AC 于点 F、G,则点 F、G 三等分 AC( ) 2. 四 边 形 ABCD中 , 点 M 、 N 分 别 在 AB 、 CD 上 若AM=BM、DN=CN 则 AD∥MN∥BC ( )3. 一组平行线,任意相邻的两平行线间的距离都相等,则 这组平行线能 等分线段。 ( )1ACG 4. 如 图l1//l2// l3且AB=BC , 那 么AB=BC=DE=EF ( ) 5.如图,DE∥BC,分别交 AB、AC 于点 D、E 则:BCDEACAEABAD ( ) 三:典型例题 1 已知线段 AB,求作:线段 AB 的五等分点。 2 如图,直角梯形 ABCD 中,AD∥BC,AB⊥BC,E 是 CD 的中点.求证 EA=EB。3. 如图,在△ABC 中,AD 是 BC 边上的中线,M 是 AD 的中点,BM 的延长线交 AC 于 N,求证:AN=CN。4 .如下图,梯形 ABCD 中,AD//BC,∠B=60°,AB=BC,E 为 AB 的中点,求证:△ECD 为等边三角形。 2CABEBEDFl3l2l1A【课堂小 结与反思】【课后作业与练习】1.已知:△ABC 中,E、G、D、F 分别是边 AB、CB 上的一点,且 GF∥ED∥AC,EF∥AD求证:.BCBDBEBG 2.已知:△ABC 中,AD 为 BC 边上的中线,过 C 任作一直线交 AD 于 E,交 AB 于 F。求证:FBAFEDAE23.如图,已知:D 为 BC 的中点,AG∥BC,求证:FCAFEDEG DCAG4.已知:△ABC 中,AD 平分∠BAC,3 求证:DCBDACAB (提示:过 C 作CE∥AD 交 BA 的延长线于 E) 5.△ABC 中,AD 平分∠BAC,CM⊥AD 交 AD 于 E...