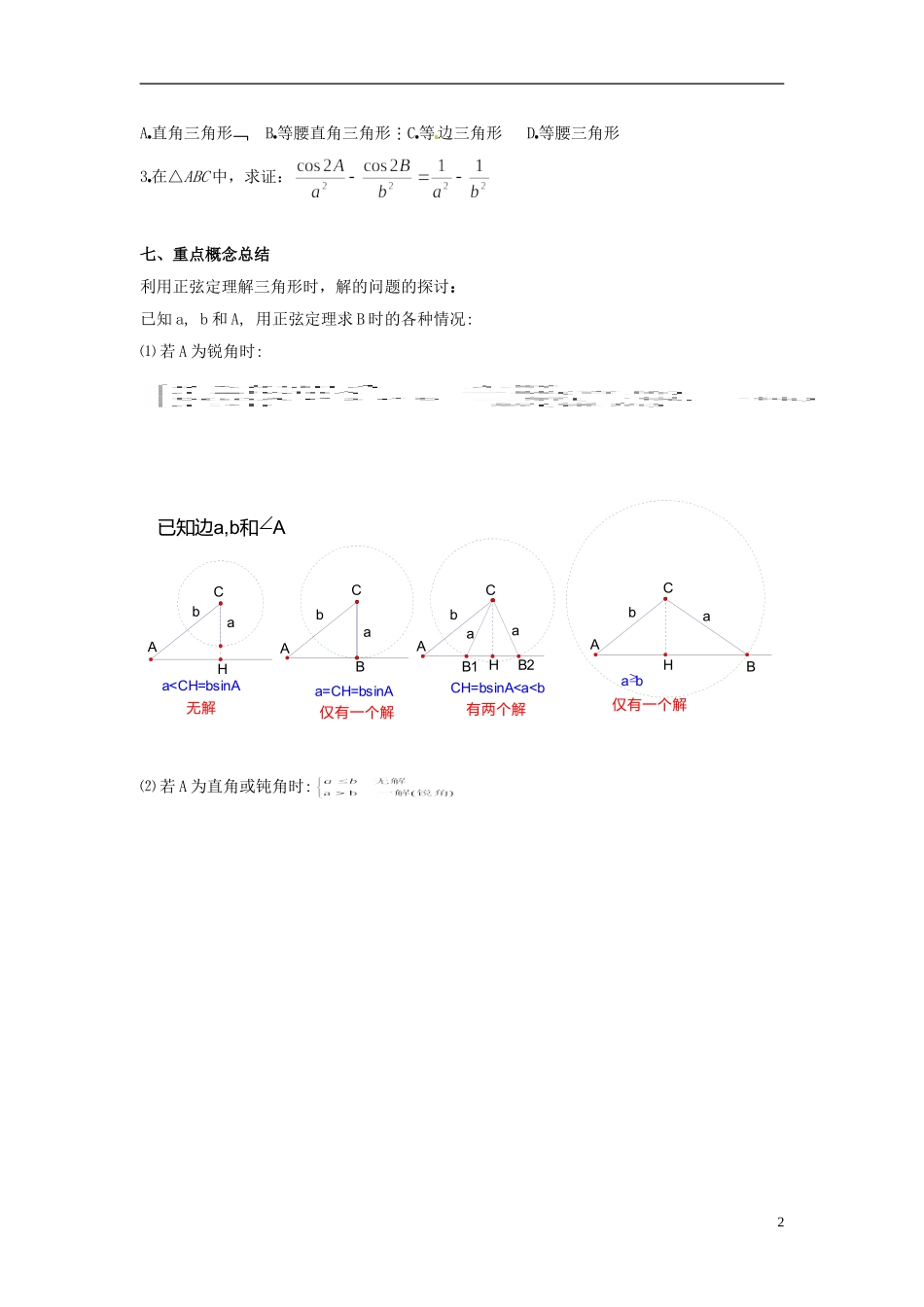
河南省淇县 2011-2012 学年高二数学上学期 1.1.1《正弦定理》导学案 沪教版一、学习目标通过对任意三角形边长和角度关系的探索,掌握正弦定理的内容及其证明方法;会运用正弦定理与三角形内角和定理解斜三角形的两类基本问题。二、本节重点正弦定理的探索和证明及其基本应用三、本节难点已知两边和其中一边的对角解三角形时判断解的个数四、知识储备1.复习:在 RtΔABC 中,C=90 ,试判定, 与之间的大小关系?2.猜想:对任意三角形 ABC 上述关系是否成立?如何证明:(1) 转化为直角三角形来证明。(2) ΔABC 的面积公式可以证明吗?(3) 能利用向量的方法来证明?五、通过预习掌握的知识点1.正弦定理: = = 正弦定理适合任意三角形,是勾股定理的推广。2.利用正弦定理,可解决两类三角形问题:(1)已知两角与一边,求另两边与另一角。(2)已知两边和其中一边的对角,求其他边角。 三角形有三条边和三个角,可看成是六个元素,则最少几个元素可能确定一个三角形。 由其中三个元素求另外三个元素的过程叫解斜三角形。 类型(2)的解的情况不唯一。六、知识运用1奎屯王新敞新疆在△ABC中,,则 k 为( )A奎屯王新敞新疆2R B奎屯王新敞新疆R C奎屯王新敞新疆4R D奎屯王新敞新疆(R 为△ABC 外接圆半径)2奎屯王新敞新疆△ABC 中,sin2A=sin2B+sin2C,则△ABC 为( )1A奎屯王新敞新疆直角三角形 B奎屯王新敞新疆等腰直角三角形C奎屯王新敞新疆等边三角形 D奎屯王新敞新疆等腰三角形3奎屯王新敞新疆在△ABC 中,求证:七、重点概念总结利用正弦定理解三角形时,解的问题的探讨:已知 a, b 和 A, 用正弦定理求 B 时的各种情况:⑴ 若 A 为锐角时:babababaa已知边a,b和A仅有一个解有两个解仅有一个解无解abCH=bsinA