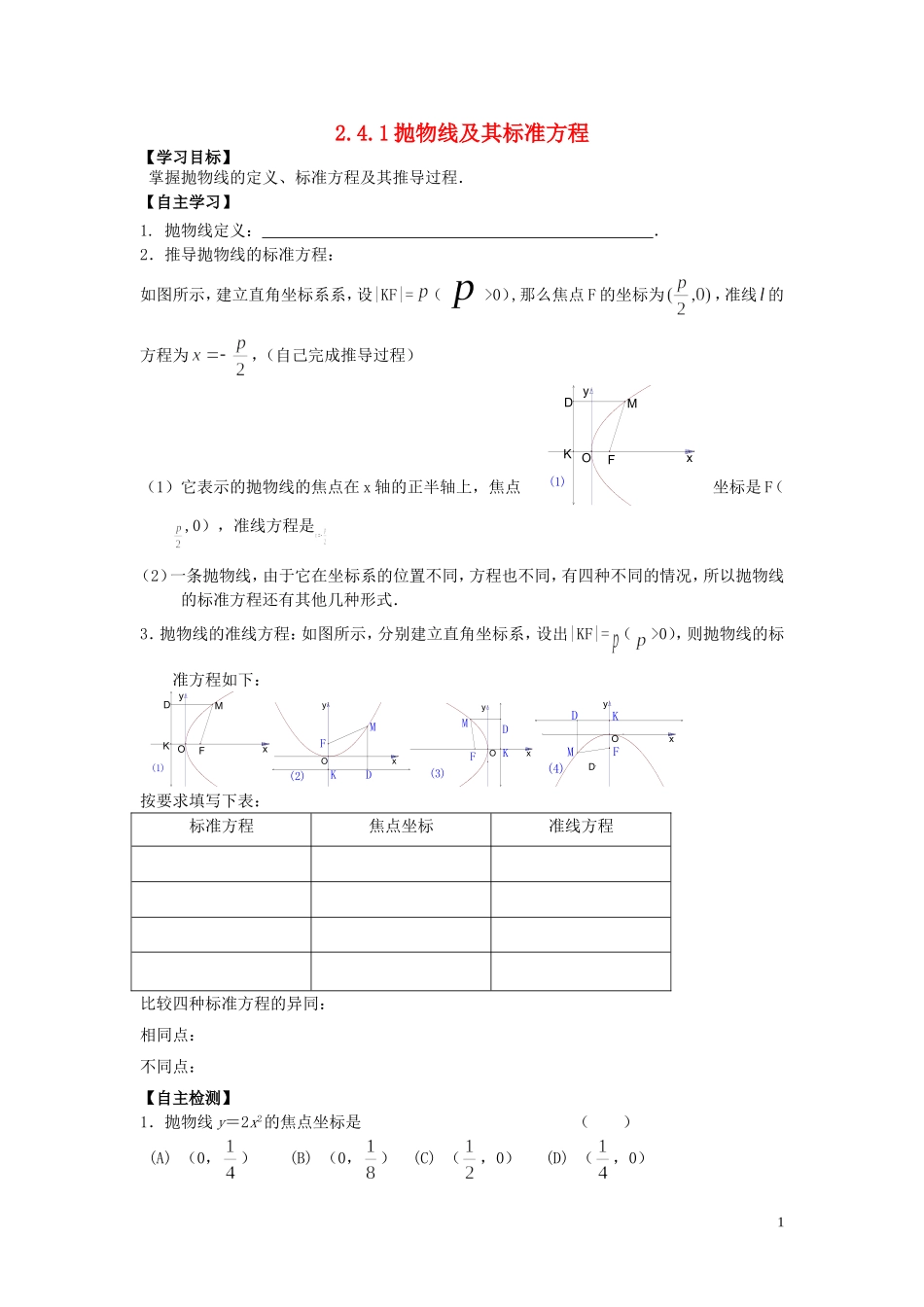
2.4.1 抛物线及其标准方程【学习目标】 掌握抛物线的定义、标准方程及其推导过程.【自主学习】1. 抛物线定义: .2.推导抛物线的标准方程:如图所示,建立直角坐标系系,设|KF|= (>0),那么焦点 F 的坐标为,准线 的方程为,(自己完成推导过程)(1)它表示的抛物线的焦点在 x 轴的正半轴上,焦点坐标是 F(,0),准线方程是 (2)一条抛物线,由于它在坐标系的位置不同,方程也不同,有四种不同的情况,所以抛物线的标准方程还有其他几种形式.3.抛物线的准线方程:如图所示,分别建立直角坐标系,设出|KF|= (>0),则抛物线的标准方程如下:xy(1)MKFODxyKDFM(2)OxyKDFM(3)OxyKDFM(4)OD按要求填写下表:标准方程焦点坐标准线方程比较四种标准方程的异同:相同点:不同点:【自主检测】1.抛物线 y=2x2的焦点坐标是 ( )(A) (0,) (B) (0,) (C) (,0) (D) (,0)1xy(1)MKFOD2.顶点在原点,焦点在 y 轴上,且过点 P(4,2)的抛物线方程是 .【典型例题】例 1 求下列抛物线方程的焦点坐标和准线方程.(1)y2=12x, (2)y=12x2,例 2 求满足下列条件的抛物线的标准方程:(1)焦点坐标是 F(-5,0),(2)焦点到准线的距离是 4,焦点在 y 轴上. 【课堂检测】1.抛物线上一点 M 的纵坐标为 4,则点 M 与抛物线焦点的距离为 .2.已知抛物线方程是,求它的焦点坐标和准线方程.2