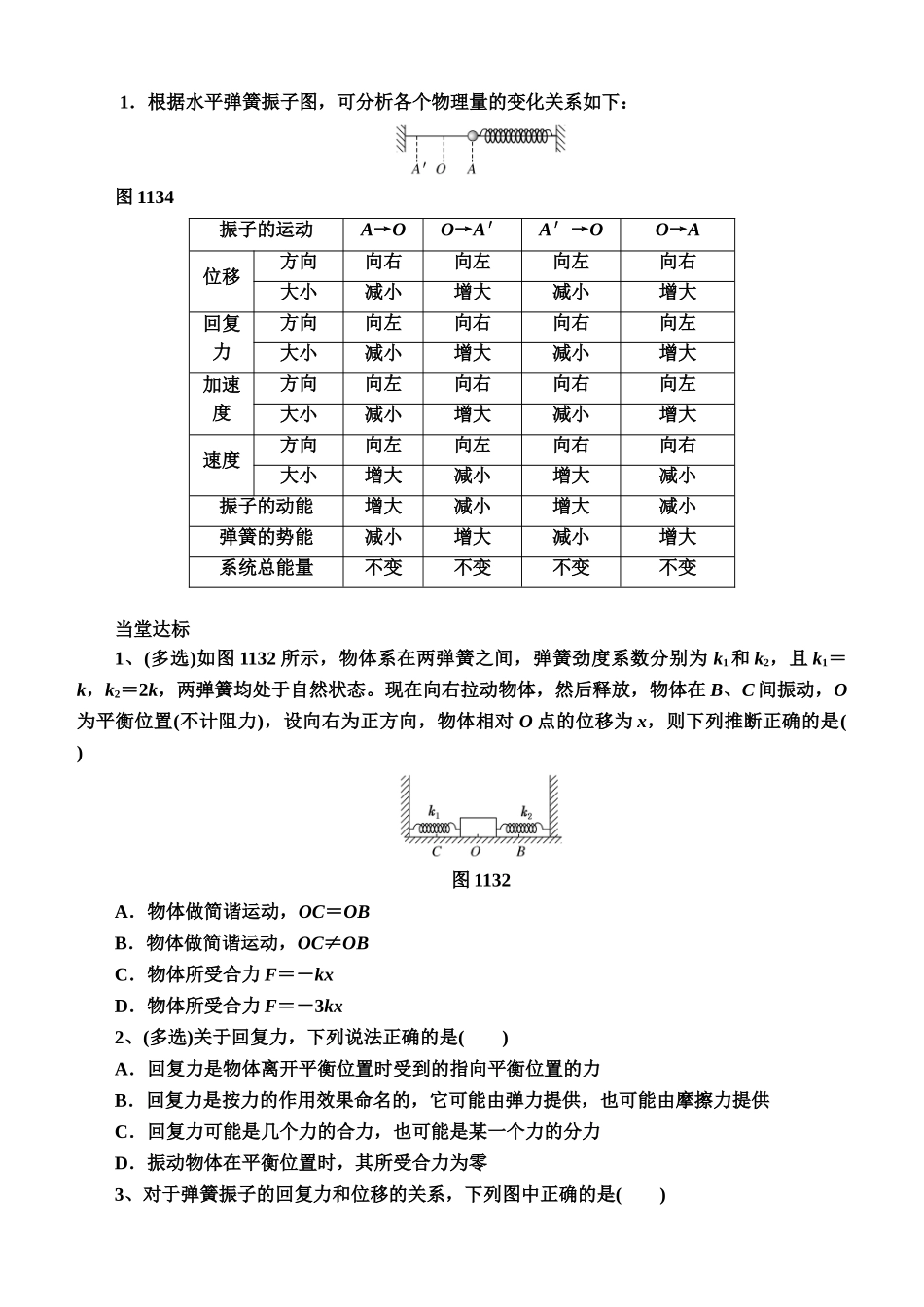
简谐运动的回复力和能量一、简谐运动的回复力1.简谐运动假如质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,质点的运动就是简谐运动。2.回复力使振动物体回到平衡位置的力。3.回复力的方向总是指向平衡位置。4.回复力的表达式F=- kx 。即回复力与物体的位移大小成正比,“-”表明回复力与位移方向始终相反,k 是一个常数,由简谐运动系统决定。二、简谐运动的能量1.振动系统(弹簧振子)的状态与能量的对应关系:弹簧振子运动的过程就是动能和势能互相转化的过程。(1)在最大位移处,势能最大,动能为零。(2)在平衡位置处,动能最大,势能最小。2.简谐运动的能量特点:在简谐运动中,振动系统的机械能守恒,而在实际运动中都有一定的能量损耗,因此简谐运动是一种理想化的模型。1.回复力的来源(1)回复力是指将振动的物体拉回到平衡位置的力,同向心力一样是根据力的作用效果来命名的。(2)回复力可以由某一个力提供,如水平弹簧振子的回复力即为弹簧的弹力;也可能是几个力的合力,如竖直悬挂的弹簧振子的回复力是弹簧弹力和重力的合力;还可能是某一力的分力。归纳起来,回复力一定等于振动物体在振动方向上所受的合力。分析物体的受力时不能再加上回复力。2.关于 k 值:公式 F=-kx 中的 k 指的是回复力与位移的比例系数,而不一定是弹簧的劲度系数,系数 k 由振动系统自身决定。3.加速度的特点:根据牛顿第二定律得 a==-x,表明弹簧振子做简谐运动时,振子的加速度大小与位移大小成正比,加速度方向与位移方向相反。4.回复力的规律:因 x=Asin(ωt+φ),故回复力 F=-kx=-kAsin(ωt+φ),可见回复力随时间按正弦规律变化。 1.根据水平弹簧振子图,可分析各个物理量的变化关系如下:图 1134振子的运动A→OO→A′A′→OO→A位移方向向右向左向左向右大小减小增大减小增大回复力方向向左向右向右向左大小减小增大减小增大加速度方向向左向右向右向左大小减小增大减小增大速度方向向左向左向右向右大小增大减小增大减小振子的动能增大减小增大减小弹簧的势能减小增大减小增大系统总能量不变不变不变不变当堂达标1、(多选)如图 1132 所示,物体系在两弹簧之间,弹簧劲度系数分别为 k1和 k2,且 k1=k,k2=2k,两弹簧均处于自然状态。现在向右拉动物体,然后释放,物体在 B、C 间振动,O为平衡位置(不计阻力),设向右为正方向,物体相对 O 点的位移为 x,则下列推断正确的是(...