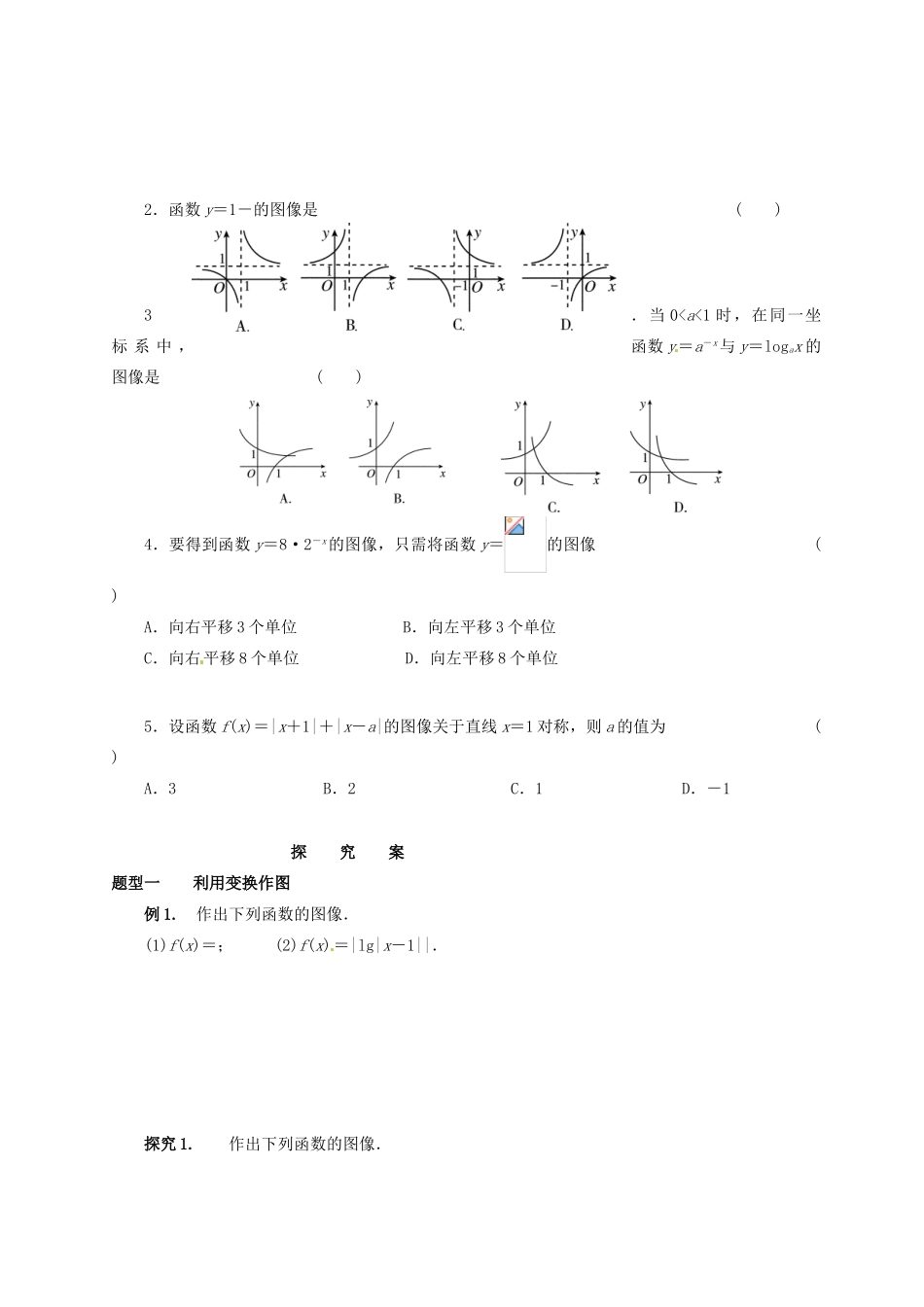
湖北省监利县第一中学 2015 届高三数学一轮复习 12.函数的图像学案【学习目标】1.掌握作函数图像的两种基本方法:描点法和图像变换法.2.了解图像的平移变换、伸缩变换、对称变换,能利用函数的图像研究函数的性质,以达到识图、作图、用图的目的. 预 习 案1.函数图像的三种变换(1)平移变换y=f(x)的图像向左平移 a(a>0)个单位,得到 的图像;y=f(x-b)(b>0)的图像可由 y=f(x)的图像 而得到;y=f(x)的图像向下平移 b(b>0)个单位,得到 的图像;y=f(x)+b(b>0)的图像可由 y=f(x)的图像 而得到.总之,对于平移变换,记忆口诀为:左加右减,上加下减.(2)对称变换y=f(-x)与 y=f(x)的图像关于 对称;y=-f(x)与 y=f(x)的图像关于 对称;y=-f(-x)与 y=f(x)的图像关于 对称;y=|f(x)|的图像可将 y=f(x)的图像在 x 轴下方的部分 ,其余部分不变而得到;y=f(|x|)的图像可先作出 y=f(x)当 x≥0 时的图像,再作关于 y 轴的对称.(3)伸缩变换y=f(ax)(a>0)的图像,可将 y=f(x)的图像上所有点的 坐标变为原来的 倍, 坐标 而得到.y=af(x)的图像,可将 y=f(x)的图像上所有点的 坐标不变, 坐标伸长为原来的 .2.几个重要结论(1)若 f(m+x)=f(m-x)恒成立,则 y=f(x)的图像关于直线 对称.(2)设函数 y=f(x)定义在实数集上,则函数 y=f(x-m)与 y=f(m-x)(m>0)的图像关于直线 对称.(3)若 f(a+x)=f(b-x),对任意 x∈R 恒成立,则 y=f(x)的图像关于 x=对称.(4)函数 y=f(a+x)与函数 y=f(b-x)的图像关于 x=对称.【预习自测】 1.函数 y=lg|x-1|的图像大致为 ( )2.函数 y=1-的图像是 ( )3.当 0