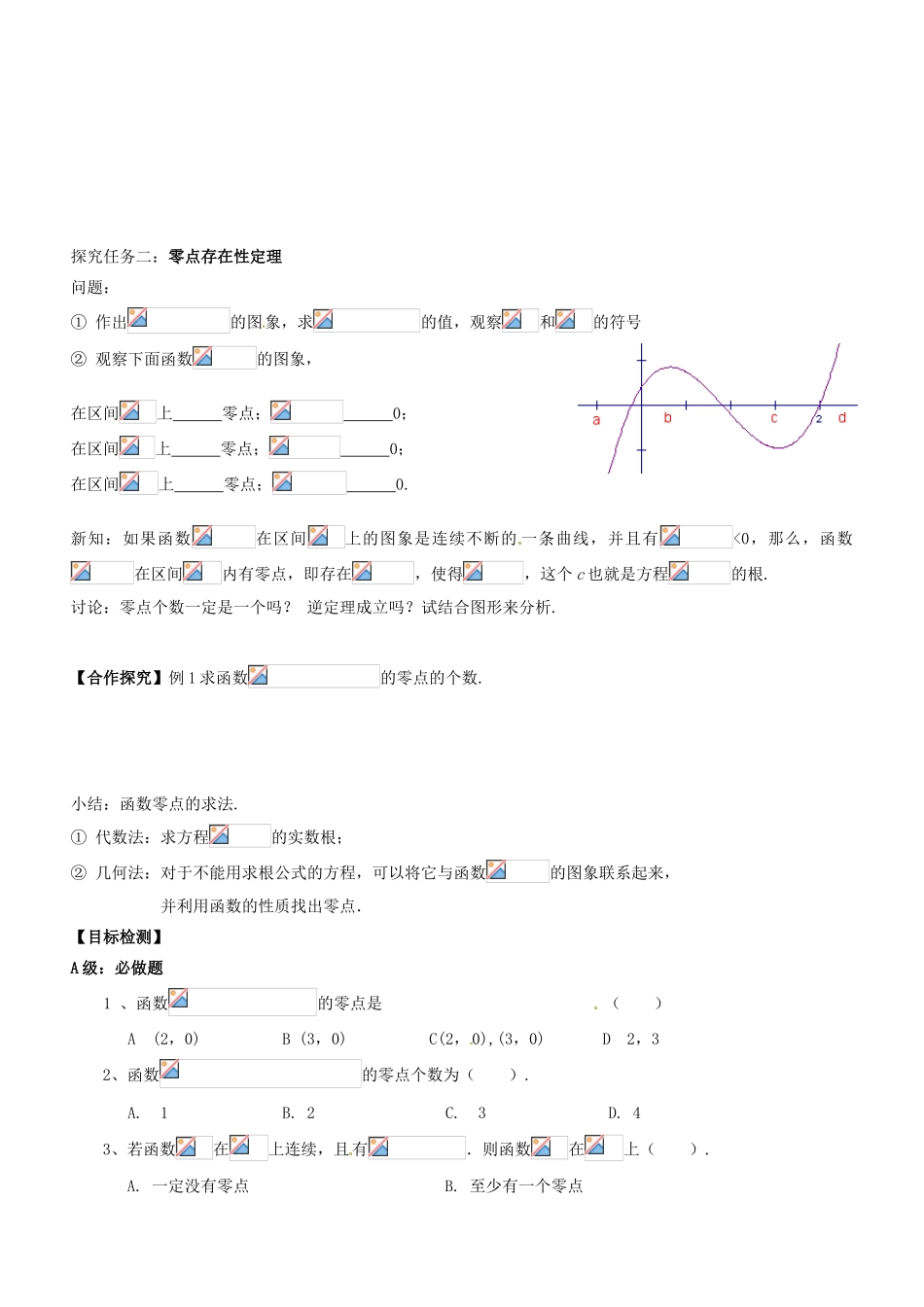
湖南省邵阳市隆回县第二中学高中数学 3.1.1 方程的根与函数的零点导学案 新人教 A 版必修 1【学习目标】1. 掌握零点的概念,理解函数的零点与方程的根的关系;2. 培养用函数观点处理问题的意识,进一步体会函数与方程思想。教学重点:方程的根与函数的零点的关系。教学难点:求函数零点的个数问题。【自主学习】阅读教材 86~87 页,思考下列问题探究任务一: 函数零点与方程的根的关系问题:① 方程的解为 ,函数的图象与 x 轴有 个交点, 坐标为 .② 方程的解为 ,函数的图象与 x 轴有 个交点, 坐标为 .③ 方程的解为 ,函数的图象与 x 轴有 个交点, 坐标为 .问题一 :试说明一元二次方程的根及其对应的二次函数的图象有怎样的关系?根据以上结论,可以得到:一元二次方程的根就是相应二次函数的图象与 x 轴交点的 .你能将结论进一步推广到吗?新知:对于函数,我们把使的实数 x 叫做函数的零点(zero point).试试:函数的零点为 ; (1)函数的零点为 .问题二:函数的零点就是方程的________,也就是函数的图象与轴交点的_________.即:方程有实数根函数的图象与轴有交点函数有零点.【合作探究】1. 求下列函数的零点: (1); (2)探究任务二:零点存在性定理问题:① 作出的图象,求的值,观察和的符号② 观察下面函数的图象,在区间上 零点; 0;在区间上 零点; 0;在区间上 零点; 0.新知:如果函数在区间上的图象是连续不断的 一条曲线,并且有<0,那么,函数在区间内有零点,即存在,使得,这个 c 也就是方程的根.讨论:零点个数一定是一个吗? 逆定理成立吗?试结合图形来分析.【合作探究】例 1 求函数的零点的个数.小结:函数零点的求法.① 代数法:求方程的实数根;② 几何法:对于不能用求根公式的方程,可以将它与函数的图象联系起来, 并利用函数的性质找出零点.【目标检测】A 级:必做题 1 、函数的零点是 ( ) A (2,0) B (3,0) C(2,0),(3,0) D 2,3 2、函数的零点个数为( ). A. 1 B. 2 C. 3 D. 43、若函数在上连续,且有.则函数在上( ). A. 一定没有零点 B. 至少有一个零点 C. 只有一个零点 D. 零点情况不确定4、函数的零点所在区间为( ). A. B. C. D. 5、Co 若函数有且仅有一个零点,求 m 的值.※ 知识拓展图象连续的函数的零点的性质:(1)函数的图象是连续的,当它通过零点时(非偶次零点),函...