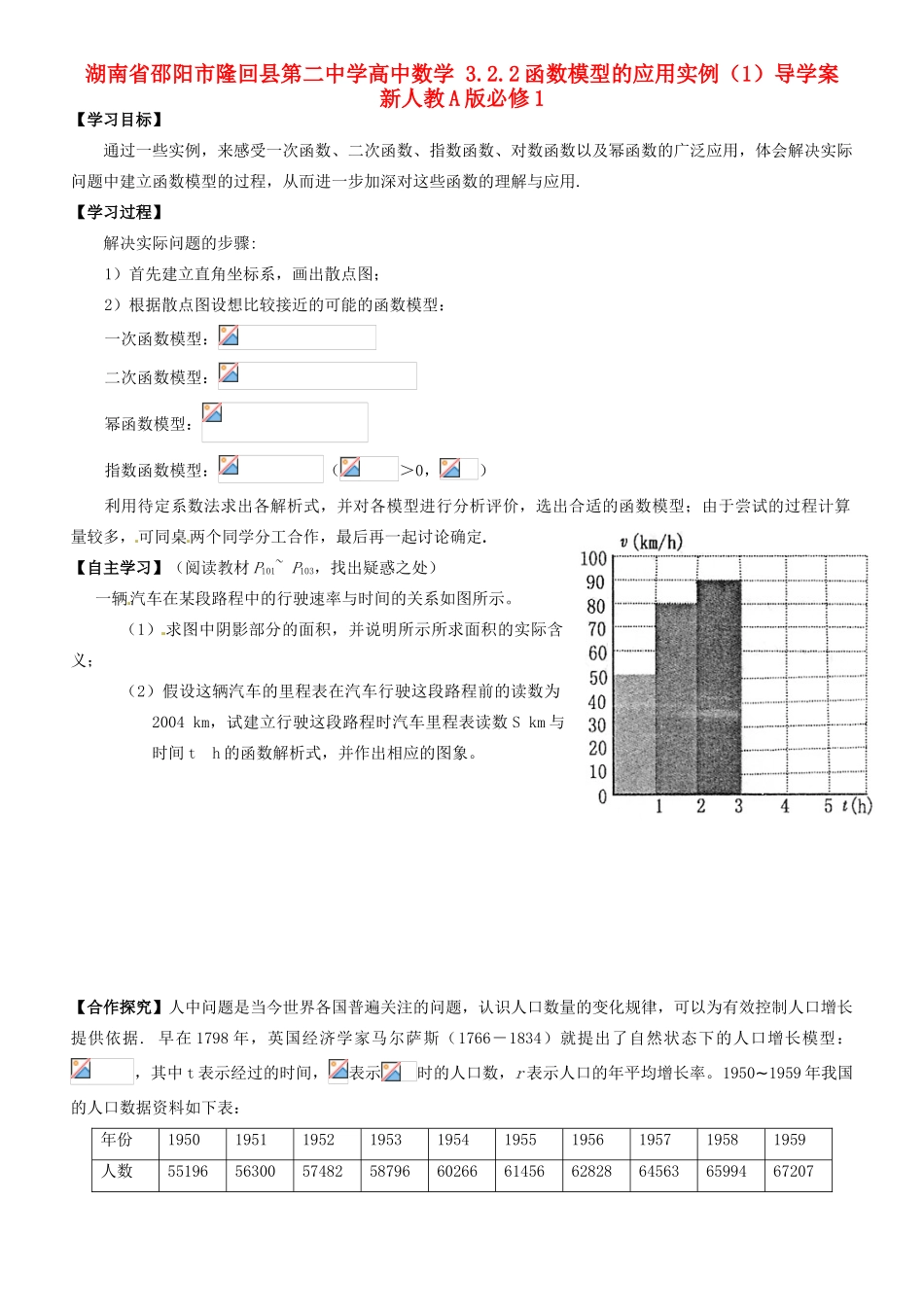
湖南省邵阳市隆回县第二中学高中数学 3.2.2 函数模型的应用实例(1)导学案 新人教 A 版必修 1【学习目标】通过一些实例,来感受一次函数、二次函数、指数函数、对数函数以及幂函数的广泛应用,体会解决实际问题中建立函数模型的过程,从而进一步加深对这些函数的理解与应用.【学习过程】解决实际问题的步骤:1)首先建立直角坐标系,画出散点图;2)根据散点图设想比较接近的可能的函数模型:一次函数模型:二次函数模型:幂函数模型:指数函数模型:(>0,)利用待定系数法求出各解析式,并对各模型进行分析评价,选出合适的函数模型;由于尝试的过程计算量较多,可同桌两个同学分工合作,最后再一起讨论确定.【自主学习】(阅读教材 P101~ P103,找出疑惑之处)一辆汽车在某段路程中的行驶速率与时间的关系如图所示。 (1) 求图中阴影部分的面积,并说明所示所求面积的实际含义; (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立行驶这段路程时汽车里程表读数 S km 与时间 t h 的函数解析式,并作出相应的图象。【合作探究】人中问题是当今世界各国普遍关注的问题,认识人口数量的变化规律,可以为有效控制人口增长提供依据. 早在 1798 年,英国经济学家马尔萨斯(1766-1834)就提出了自然状态下的人口增长模型:,其中 t 表示经过的时间,表示时的人口数,r 表示人口的年平均增长率。19501959∼年我国的人口数据资料如下表:年份1950195119521953195419551956195719581959人数55196563005748258796602666145662828645636599467207/万人1)如果各年人口增长率的表彰会值作为我国这一时期的人口增长率(精确到 0.0001),用马尔萨其余人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;2)如果按上表的增长情况,大约在哪一年我国的人口达到 13 亿?【目标检测】(A 级:必做题1. 按复利计算,若存入银行 5 万元,年利率 2%,3 年后支取, 则可得利息(单位 :万元) 为( ).A. 5(1+0.02) B. 5(1+0.02) C. 5(1+0.02) -5 D.5(1+0.02) -52. x 克 a%盐水中,加入 y 克 b%的盐水,浓度变为 c%,则 x与 y 的函数关系式为( ).A. y=x B. y=x C. y=x D. y=x3. A、B 两家电器公司在今年 1—5 月份的销售量如下图所示, 则 B 相对于A 其市场份额比例比较大的月份是( ). A. 2 月 B. 3 月 C. 4 月 D. 5...