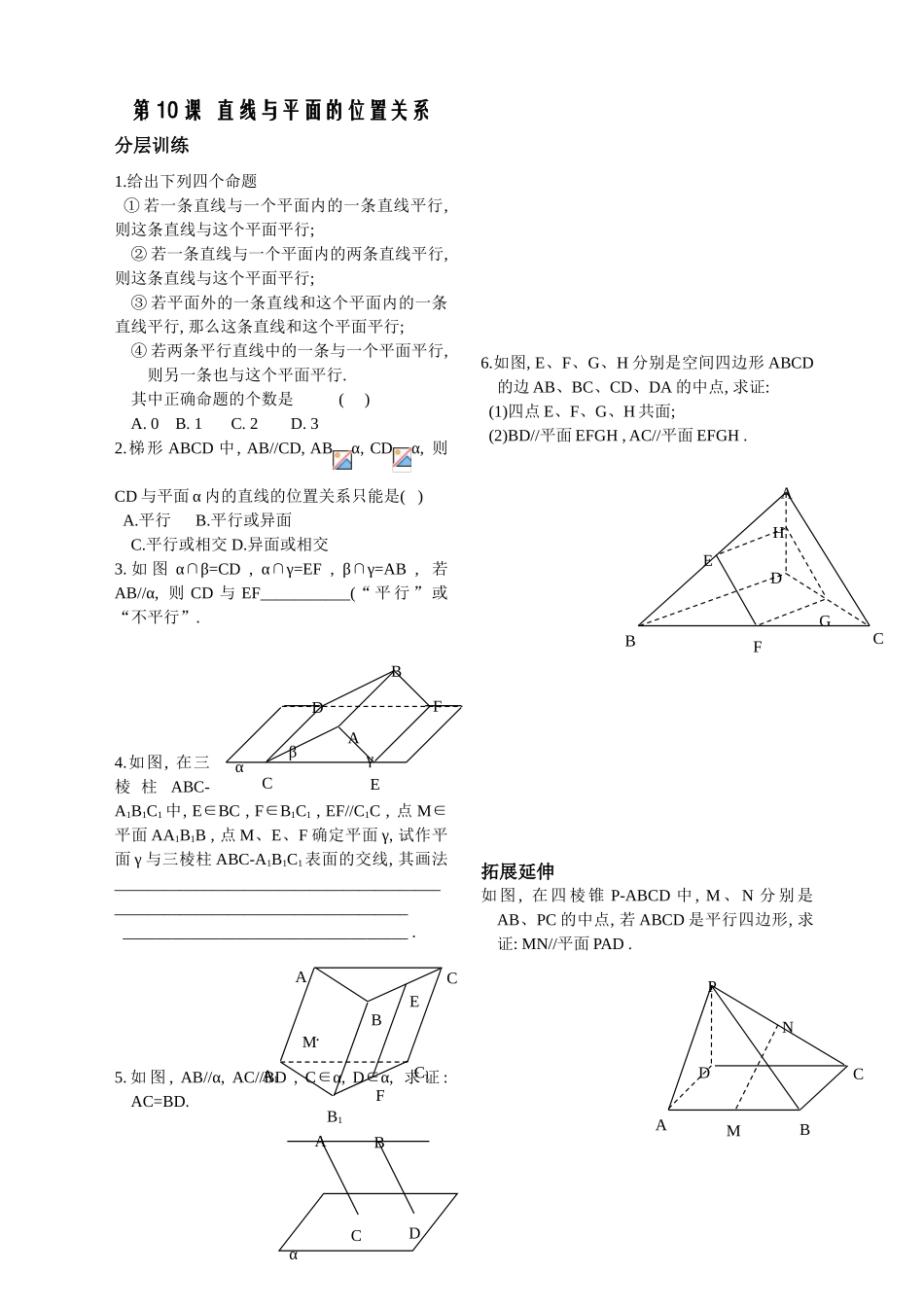
第 10 课 直线与平面的位置关系分层训练1.给出下列四个命题 ① 若一条直线与一个平面内的一条直线平行, 则这条直线与这个平面平行;② 若一条直线与一个平面内的两条直线平行, 则这条直线与这个平面平行;③ 若平面外的一条直线和这个平面内的一条直线平行, 那么这条直线和这个平面平行;④ 若两条平行直线中的一条与一个平面平行, 则另一条也与这个平面平行.其中正确命题的个数是 ( ) A. 0 B. 1 C. 2 D. 32.梯形 ABCD 中, AB//CD, ABα, CDα, 则CD 与平面 α 内的直线的位置关系只能是( ) A.平行 B.平行或异面 C.平行或相交 D.异面或相交 3. 如 图 α∩β=CD , α∩γ=EF , β∩γ=AB , 若AB//α, 则 CD 与 EF___________(“ 平 行 ” 或“不平行”.4.如图, 在三棱 柱ABC-A1B1C1 中, E∈BC , F∈B1C1 , EF//C1C , 点 M∈平面 AA1B1B , 点 M、E、F 确定平面 γ, 试作平面 γ 与三棱柱 ABC-A1B1C1表面的交线, 其画法____________________________________________________________________________ ___________________________________ .5. 如 图 , AB//α, AC//BD , C∈α, D∈α, 求 证 : AC=BD.6.如图, E、F、G、H 分别是空间四边形 ABCD的边 AB、BC、CD、DA 的中点, 求证: (1)四点 E、F、G、H 共面; (2)BD//平面 EFGH , AC//平面 EFGH .拓展延伸如 图 , 在 四 棱 锥 P-ABCD 中 , M 、 N 分 别 是AB、PC 的中点, 若 ABCD 是平行四边形, 求证: MN//平面 PAD .·MACC1B1A1FBEACFBEHDGPNCBAMDBFDCEαβγACDBAα节学习疑点:学生质疑教师释疑