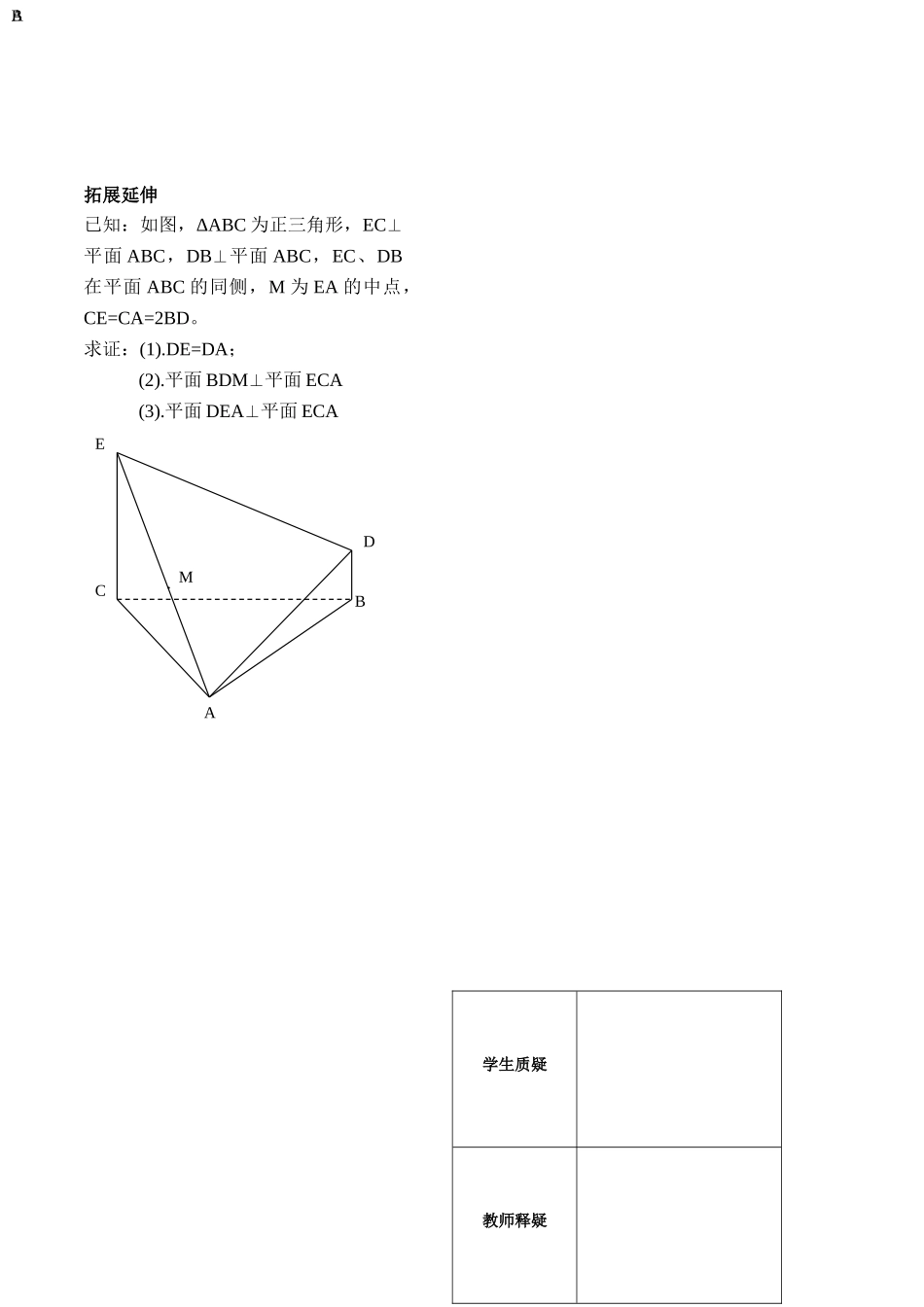
第 15 课时 平面与平面垂直分层训练1.一条直线与两个平面所成角相等, 那么这两个平面的位置关系是( ) A.平行 B.相交 C.平行或相交 D.以上都不对2.设 m 、n 是两条不同的直线, α、β、γ 是三个不同的平面, 给出下列四个命题: ① 若 m⊥α, n //α, 则 m⊥n ; ② 若 α//β, β//γ, m⊥α, 则 m⊥γ;③ 若 m //α, n //α, 则 m // n ; ④ 若 α⊥γ, β⊥γ, 则 α//β.其中正确命题的序号是 ( )A. ① ② B. ② ③ C. ③ ④ D. ① ④3.在空间四边形ABCD中AD⊥BC,BD⊥AD,且三角形 BCD 是锐角三角形,那么必有( )A.平面 ABD⊥平面 ADC B. 平面 ABD⊥平面 ABC C. 平面 ADC⊥平面 BCD D. 平面 ABC⊥平面 BCD4.已知平面 α⊥β, α∩β= l , P 是空间一点, 且 P到 α、β 的距离分别是 1、2 , 则点 P 到 l 的距离为_____________ .5.已知点 A(3 , 2) , B(-2 , -3), 沿 y 轴把直角坐标平面折成 90°的二面角后, AB 的长为____________ .6.如图, α⊥β,α∩β= l , ABα, AB⊥l, BCβ, DEβ, BC⊥DE , 求证: AC⊥DE .7在正方体 ABCD-A1B1C1D1 中, 求证: 平面B1AC⊥面 B1D1DB .ABECDαβlABCDD1A1B1C1拓展延伸已知:如图,ΔABC 为正三角形,EC⊥平面 ABC,DB⊥平面 ABC,EC、DB在平面 ABC 的同侧,M 为 EA 的中点,CE=CA=2BD。求证:(1).DE=DA;(2).平面 BDM⊥平面 ECA(3).平面 DEA⊥平面 ECA学生质疑教师释疑ADCBEAMB.