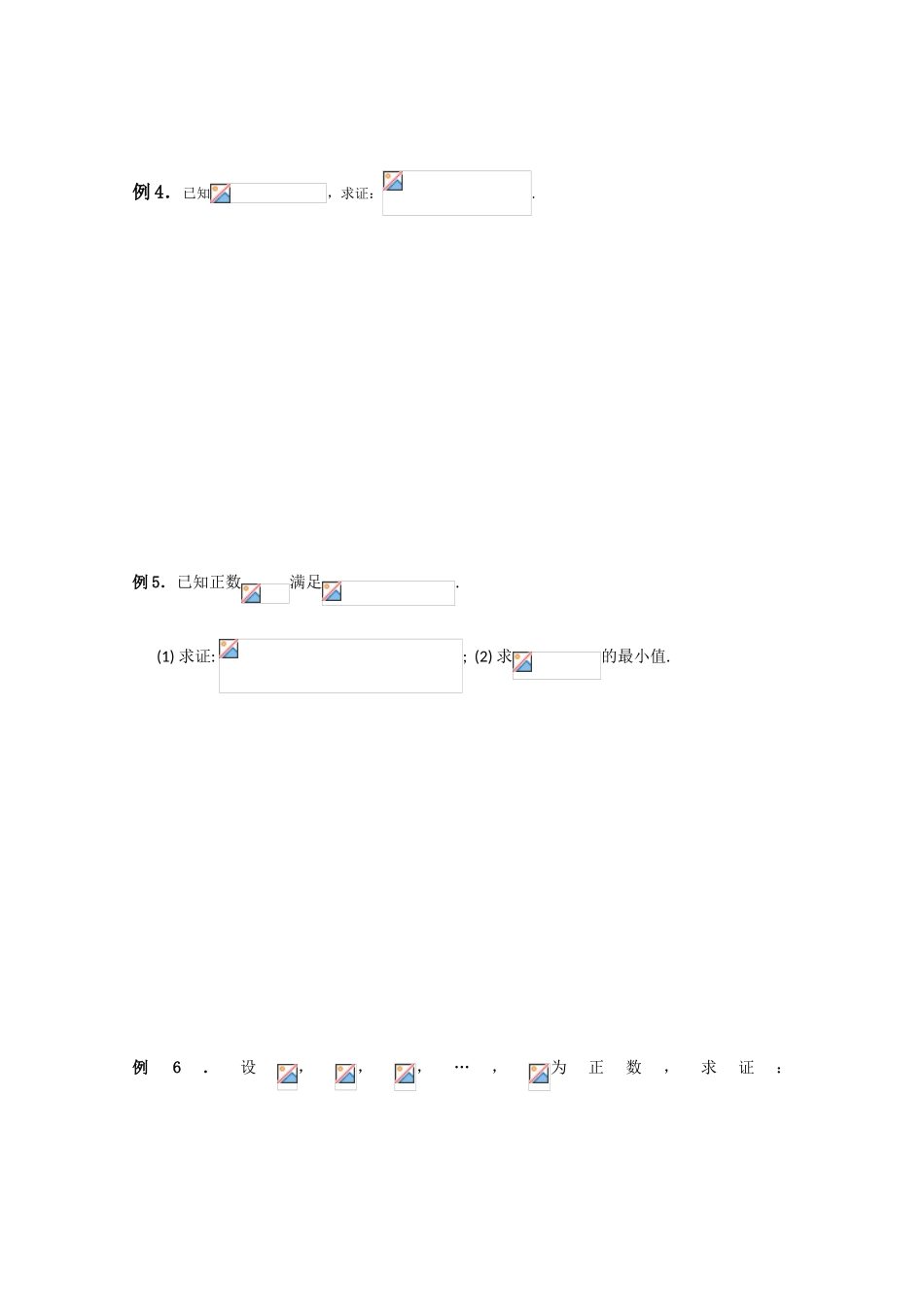
《不等式选讲》复习学案 §1.4 10 届考点模拟(2) 姓名 考点一. 绝对值的几何意义,解含参绝对值不等式的解法 例 1.不等式的解集为__________________.考点二.均值不等式、柯西不等式应用. 例 2.设的三边长分别为,(1)判定 的符号;(2)求证:. 例 3.已知,证明不等式: (1); (2).例 4.已知,求证:.例 5.已知正数满足.(1) 求证: ; (2) 求的最小值.例6.设,,,…,为正数,求证:. 例 7.已知,且。 求证:答案:例 1.解析: 当≤-2 时,原不等式可以化为≥5,解得≤-3, 即不等式组的解集是. 当时,原不等式可以化为≥5,即 3≥5,矛盾.所以不等式组,的解集为, 当≥1 时,原不等式可以化为≥5,解得≥2, 即不等式组的解集是. 综上所述,原不等式的解集是; 答案:例 2.解析:(1)因为的三角形的三边,所以……4分(2) 例 3.证明:(1)由均值不等式可得,即,故所证成立. 5 分 (2)因为 ①, ②, ③ ①②③ 式两边相加,得 即,故所证成立. 10分例 4.【解】因为,所以,所以要证, 即证, 即证, 即证,而显然成立,故.…… 10 分 例 5.(1) 解: 根据柯西不等式,得, 因为,所以. … 5 分(2) 解: 根据均值不等式, 得,当且仅当时, 等号成立. 根据柯西不等式, 得, 即 , 当且仅当时, 等号成立. 综上, .当且仅当,,时, 等号成立。所以的最小值为 18 .… 10 分