课时提升作业(三十五)二元一次不等式(组)与简单的线性规划问题(25分钟50分)一、选择题(每小题5分,共35分)1.已知点(-3,-1)和点(4,-6)在直线3x-2y-a=0的两侧,则a的取值范围为()A.(-24,7)B.(-7,24)C.(-∞,-7)(24,+∞)∪D.(-∞,-24)(7,+∞)∪【解析】选B.根据题意知(-9+2-a)·(12+12-a)<0,即(a+7)(a-24)<0,解得-7
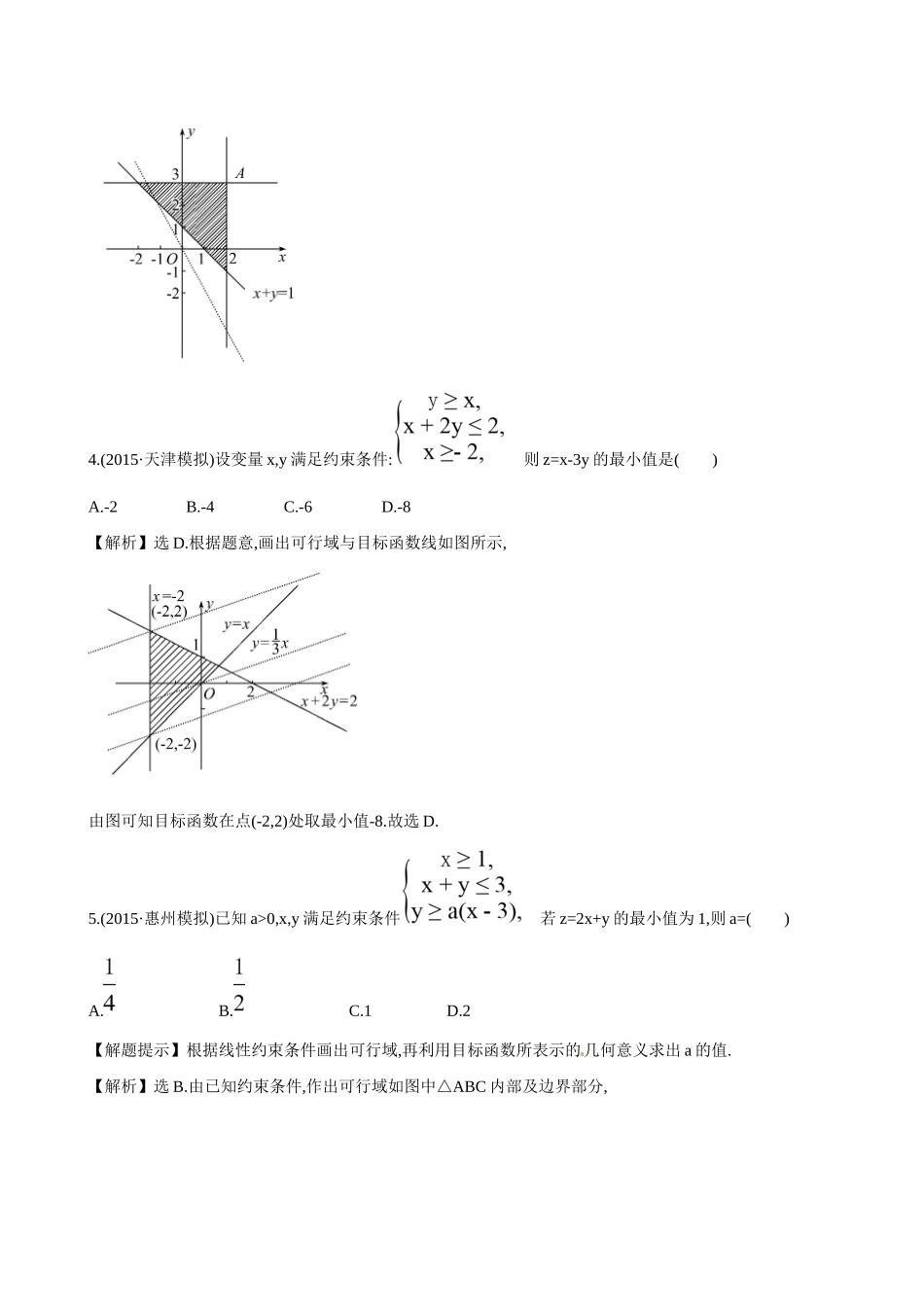
2,即2m+n<4,所以m+n<2,即m+n-2<0,所以点(m,n)必在直线x+y-2=0的左下方.3.(2015·岳阳模拟)若实数x,y满足则S=2x+y-1的最大值为()A.6B.4C.3D.2【解析】选A.作出的可行域将S=2x+y-1变形为y=-2x+S+1,作直线y=-2x平移至点A(2,3)时,S最大,将x=2,y=3代入S=2x+y-1得S=6.4.(2015·天津模拟)设变量x,y满足约束条件:则z=x-3y的最小值是()A.-2B.-4C.-6D.-8【解析】选D.根据题意,画出可行域与目标函数线如图所示,由图可知目标函数在点(-2,2)处取最小值-8.故选D.5.(2015·惠州模拟)已知a>0,x,y满足约束条件若z=2x+y的最小值为1,则a=()A.B.C.1D.2【解题提示】根据线性约束条件画出可行域,再利用目标函数所表示的几何意义求出a的值.【解析】选B.由已知约束条件,作出可行域如图中△ABC内部及边界部分,由目标函数z=2x+y的几何意义为直线l:y=-2x+z在y轴上的截距,知当直线l过可行域内的点B(1,-2a)时,目标函数z=2x+y的最小值为1,则2-2a=1,a=.故选B.6.(2015·南昌模拟)若关于x,y的不等式组(a为常数)所表示的平面区域的面积等于2,则a的值为()A.1B.2C.3D.-1【解析】选C.当a≤0时,显然不合题意;当a>0时,不等式组所围成的区域如图所示.因为其面积为2,所以|AC|=4,所以C的坐标为(1,4),代入ax-y+1=0,解得a=3.【加固训练】(2014·合肥模拟)平面区域的面积是()A.B.C.D.【解析】选A.作出不等式组对应的平面区域如图,则区域是圆心角为的扇形,故面积是×π×2=,故选A.7.(2015·郑州模拟)设z=x+y,其中实数x,y满足若z的最大值为12,则z的最小值为()A.-3B.-6C.3D.6【解析】选B.可行域如图:由得A(k,k),目标函数z=x+y在x=k,y=k时取最大值,即直线z=x+y在y轴上的截距z最大,此时,12=k+k,故k=6,所以得B(-12,6),目标函数z=x+y在x=-12,y=6时取最小值,此时,z的最小值为z=-12+6=-6,故选B.二、填空题(每小题5分,共15分)8.(2015·抚顺模拟)若点(x,y)在不等式组表示的平面区域内运动,则t=x-y的取值范围是.【解析】先根据约束条件画出可行域,由得B(2,0),由得A(0,1),当直线t=x-y过点A(0,1)时,t最小,t最小是-1,当直线t=x-y过点B(2,0)时,t最大,t最大是2,则t=x-y的取值范围是[-1,2].答案:[-1,2]9.(2015·衡阳模拟)已知点P(t,2)在不等式组所表示的平面区域内运动,l为过点P和坐标原点O的直线,则l的斜率的取值范围为.【解析】由不等式组可得所表示的可行域,由图可知:当取点P(1,2)时,直线l的斜率取得最大值,k==2.当取点P(2,2)时,直线l的斜率取得最小值,k==1,故k[1,2].∈答案:[1,2]10.已知实数x,y满足若z=y-ax取得最大值时的最优解(x,y)有无数个,则a=.【解析】依题意,在坐标平面内画出题中的不等式组表示的平面区域,如图所示.要使z=y-ax取得最大值时的最优解(x,y)有无数个,则直线z=y-ax必平行于直线y-x+1=0,于是有a=1.答案:1【误区警示】此题经常出现两种情况:一是找不到解题的思路;二是最优解有无数个,说明目标函数对应的直线和边界平行,容易把边界判断错误导致结果不对.(20分钟40分)1.(5分)(2014·山东高考)已知x,y满足约束条件当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2时,a2+b2的最小值为()A.5B.4C.D.2【解析】选B.解方程组求得交点为,则2a+b=2,a2+b2的最小值即为在直线2a+b=2上找一点,使得它到原点的距离的平方最小.即求点到直线2a+b=2的距离的平方为=22=4.2.(5分)(2013·北京高考)设D为不等式组表示的平面区域,区域D上的点与点(1,0)之间的距离的最小值为.【解析】不等式组表示的平面区域如图所示,可得点(1,0)到区域D上点的最小距离即是点(1,0)到直线2x-y=0的距离,d==.答案:3.(5分)(2015·长沙模拟)已知x,y满足约束条件则x2+4y2的最小值是.【...