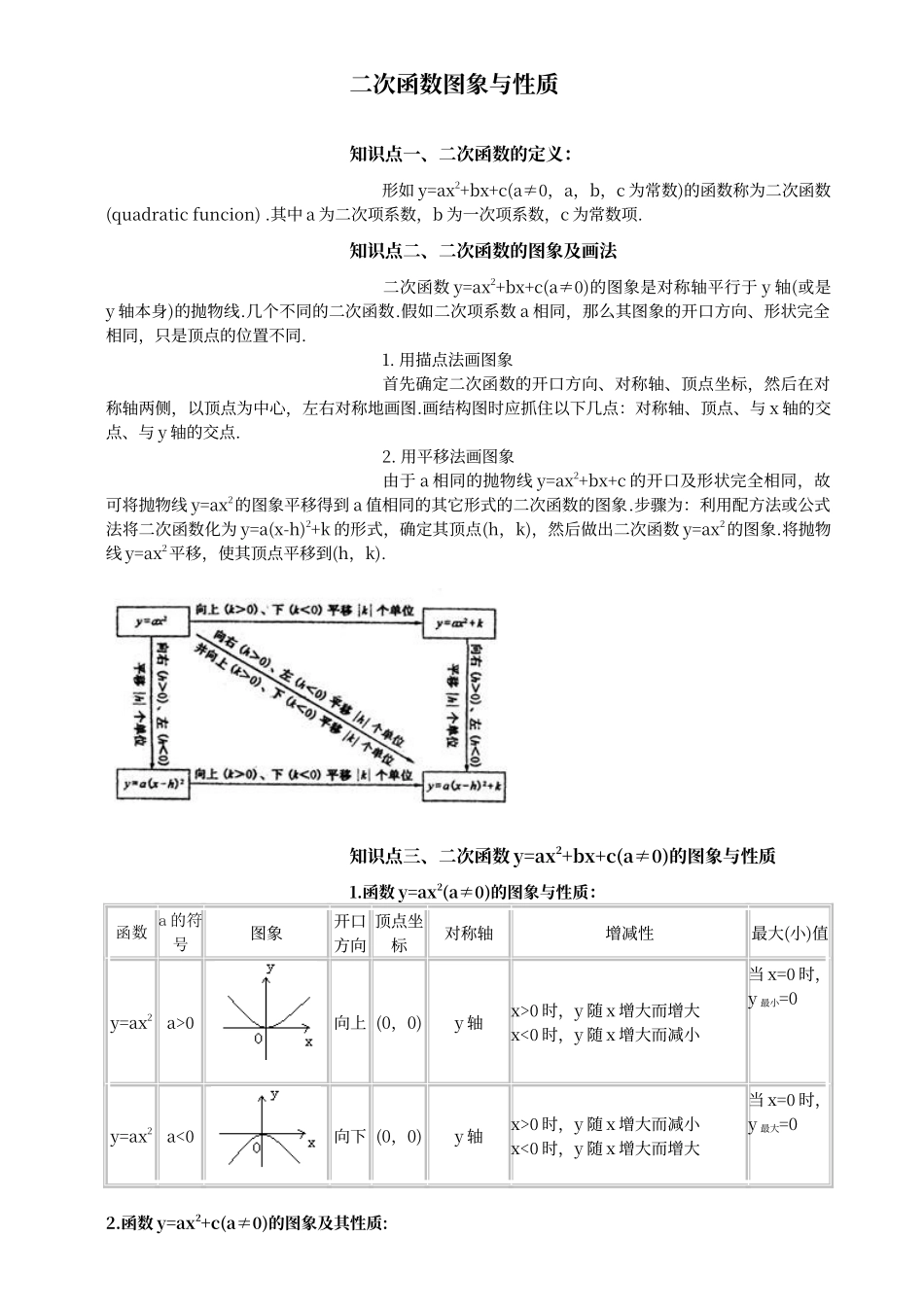
二次函数图象与性质知识点一、二次函数的定义: 形如 y=ax2+bx+c(a≠0,a,b,c 为常数)的函数称为二次函数(quadratic funcion) .其中 a 为二次项系数,b 为一次项系数,c 为常数项.知识点二、二次函数的图象及画法 二次函数 y=ax2+bx+c(a≠0)的图象是对称轴平行于 y 轴(或是y 轴本身)的抛物线.几个不同的二次函数.假如二次项系数 a 相同,那么其图象的开口方向、形状完全相同,只是顶点的位置不同. 1. 用描点法画图象 首先确定二次函数的开口方向、对称轴、顶点坐标,然后在对称轴两侧,以顶点为中心,左右对称地画图.画结构图时应抓住以下几点:对称轴、顶点、与 x 轴的交点、与 y 轴的交点. 2. 用平移法画图象 由于 a 相同的抛物线 y=ax2+bx+c 的开口及形状完全相同,故可将抛物线 y=ax2的图象平移得到 a 值相同的其它形式的二次函数的图象.步骤为:利用配方法或公式法将二次函数化为 y=a(x-h)2+k 的形式,确定其顶点(h,k),然后做出二次函数 y=ax2的图象.将抛物线 y=ax2平移,使其顶点平移到(h,k). 知识点三、二次函数 y=ax2+bx+c(a≠0)的图象与性质1.函数 y=ax2(a≠0)的图象与性质:函数 a 的符号图象开口方向顶点坐标对称轴增减性最大(小)值y=ax2a>0向上 (0,0)y 轴x>0 时,y 随 x 增大而增大x<0 时,y 随 x 增大而减小当 x=0 时,y 最小=0y=ax2a<0向下 (0,0)y 轴x>0 时,y 随 x 增大而减小x<0 时,y 随 x 增大而增大当 x=0 时,y 最大=02.函数 y=ax2+c(a≠0)的图象及其性质: (1)当 a>0 时,开口方向、对称轴、增减性与 y=ax2相同,不同的是顶点坐标为(0,c),当 x=0 时,y 最小=c (2)当 a<0 时,开口方向、对称轴、增减性与 y=ax2相同,不同的是顶点坐标为(0,c),当 x=0 时,y 最大=c3.二次函数 y=ax2+bx+c(a≠0)的图象与性质: 二次函数 y=ax2+bx+c(a≠0)的图象是一条抛物线.它的顶点坐标是, 对称轴是直线函数二次函数 y=ax2+bx+c(a,b,c 是常数,a≠0)图象a>0a<0性质(1)当 a>0 时,抛物线开口向上,并向上无限延伸,顶点是它的最低点.(2)在对称轴直线的左侧,抛物线自左向右下降,在对称轴的右侧,抛物线自左向右上升.(1)当 a<0 时,抛物线开口向下,并向下无限延伸,顶点是它的最高点.(2)在对称轴直线的左侧,抛物线自左向右上升;在对称轴右侧,抛物线自左向右下降.知识点四、抛物线 y=ax2+bx+c 中 a、b、c 的作用a,b,c 的...